Rozwiąż nierówność
kamil: Rozwiąż nierówność 32+2x−1≤0
11 cze 17:44
Mila:
Może
3x2+2x−1≤0
11 cze 17:45
kamil: dokładnie
11 cze 17:46
kamil: niestety nie ma możliwości edycji postu a chciałbym sprawdzić czy prawidłowo rozwiązałem
równanie
11 cze 17:49
6-latek:
Δ=2
2+4*3
Δ=16
√Δ=4
x∊<−3,1>
11 cze 18:09
zadanko: | | −2 − 4 | | −2 − 4 | |
a dlaczego x1 = |
| nie powinno być x1 = |
| ? z racji tego że |
| | 2 | | 6 | |
11 cze 18:16
6-latek: racja to popraw sobie
11 cze 18:17
kamil: | | 1 | |
a jakie wyjdą przedziały ? x≤0 ∊ (−∞ ; −1> U < |
| ; +∞) |
| | 3 | |
11 cze 18:20
Mila:
3x
2+2x−1≤0
Δ=4+4*3*1=16
√16=4
| | −2−4 | | −2+4 | |
x1= |
| lub x2= |
| |
| | 6 | | 6 | |
a=3 >0 parabola skierowana ramionami do góry ( rysunek masz u góry)
11 cze 18:22
kamil: Dziękuję
11 cze 18:24
Mila: 
11 cze 18:25
kamil: mam jeszcze jedno pytanko do rysunku, jak opisać przedziały monotoniczności funkcji ?
11 cze 18:43
Mila:
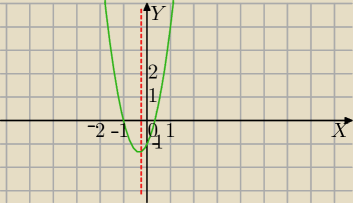
f(x)=3x
2+2x−1
x
w − to argument w którym zmienia się typ monotoniczności.
| | −b | | −2 | | −1 | |
xw= |
| = |
| = |
| pierwsza wsp. wierzchołka paraboli |
| | 2a | | 6 | | 3 | |
| | −1 | | −1 | |
dla x< |
| funkcja malejąca⇔dla x∊(−∞, |
| )− funkcja malejąca |
| | 3 | | 3 | |
| | −1 | |
dla x∊( |
| ,∞) − funkcja rosnąca |
| | 3 | |
11 cze 19:29
kamil: zawsze będą przedziały otwarte ?
11 cze 19:48