Trygonometria, sumy i różnice kątów, podwojony kąt lulu:

	α		4
1) Wiedząc że sin		=		i α∊ 90−180 stopni oblicz:
	2		5

sinα, cosα, tgα, ctgα 2) wiedząc że tg2α= −3 oblicz sin4α i cos4α Proszę o pomoc. Nie bardzo wiem jak mam tu wzory zastosować

lulu: Pomoże ktoś?

Mila: 1) sin²x+cos²x=1

	α		α
sin2		+cos2		=1⇔
	2		2

16		α
	+cos2		=1
25		2

	α		9
cos2		=
	2		25

	α		3
cos		=
	2		5

	α		α
2*sin		*cos		=sinα [ wzór: sin2x=2sinx *cosx]
	2		2

	4		3
2*		*		=sinα
	5		5

	24
sinα=		(kąt α∊ drugiej ćwiartki, to sinα>0)
	25

Dalej z jedynki trygonometrycznej liczysz cos α, pamiętając, że jest ujemny w drugiej ćwiartce.

Eta:

	α		4		α
1/ sin		=		, cos		=............
	2		5		2

i teraz:

	α		α
sinα=2sin		*cos		=...
	2		2

	α
cosα= 1−2sin2		=.........
	2

	sinα
tgα=		=..........
	cosα

	1
ctgα=		=..........
	tgα

2/ tg2α= −3 ⇒ sin2α=......... i cos2α=......... sin4α= 2sin2α*cos2α=....... cos4α= 1−2sin²2α=.......

Eta:

lulu: Ale w tym drugim to co mam podstawic do wzoru na sin i cos?

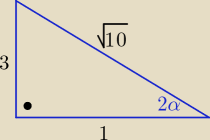Eta: tg2α= −3 <0 to 2α€ II ćw v IVćw

	3√10		3√10
sin2α=		v sin2α= −
	10		10

	√10		√10
cos2α= −		v cos2α=
	10		10