Pole ograniczone liniami Kornelka: Oblicz pole ograniczone liniami y= x² − 2, y=0. 2. obszar ograniczony liniami y=x y=√4−x², y=0 Opisz jako normalny względem osi OY, w układzie biegunowym.

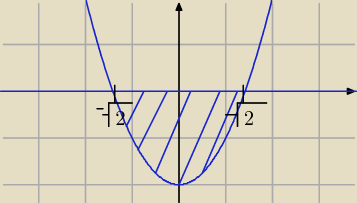
Vizer: 1. (rysunek) Przecięcie się krzywych x² − 2 = 0 (x − √2)(x + √2) = 0 x = √2 v x = −√2 Wiemy, że dla tego przedziału, prosta y = 0 jest "wyżej" od paraboli y = x² − 2. Pole więc wyraża się wzorem : ∫^√2_−√2 (0 − x² + 2) dx = ... Albo za pomocą całki podwójnej : ∫^√2_−√2 dx ∫⁰_x²−2 dy = ...

karusiaaa: Źle obliczyłam całkę i mi się wyzerowało, dlatego nie wiedziałam gdzie jest błąd.. Dzięki wielkie

karusiaaa: Pomożesz przy tym drugim? Obszar normalny względem osi OY wyszedł mi taki ∫ od 0 do √2 dy ∫ od y do √4−y f (x,y) dx.. Tylko nie wiem czy dobrze i co z tą zamianą na układ biegunowy.

Vizer: Wydaje się dobrze, tylko pewnie literówka przy górnej granicy w drugiej całce √4 − y² powinno być. A co do współrzędnych biegunowych to wiedząc, że masz do czynienia z okręgiem x² + y² = 4 to 0 ≤ r ≤ 2 (podstawiając do równania okręgu wsp. biegunowe : r²cos²φ + r²sin²φ = 4, wyliczając r dostajesz granice całkowania)

	π		π
0 ≤ φ ≤		(kąt się zmienia do		bo y = x nachylona pod tym kątem)
	4		4

Całka: ∫π40 dφ ∫20 f(x,y) dr

karusiaaa: Dzięki

karusiaaa: A jeszcze mam takie zadanie oblicz całkę podwójną dxdy gdzie D− obszar ograniczony liniami y=x, y=1, x=0, to najpierw wyznaczam sobie obszar jako normalny względem osi OX albo OY a później wyznaczam wzór tego obszaru czyli funkcja nakrywająca i funkcja ograniczająca z dołu?

Vizer: Tak

Vizer: Możesz przedstawić tu swój wynik, sprawdzę

Patryk: chyba zaznaczam zły obszar i nie chce mi coś wyjść dobrze..