nierówności wielomianów Perpetuo: 5x³−21x²−21x+5≥0

	5
mi x=		; x=−1
	21

	1
a w odp są użyte m.in. −1,		,5
	5

Eta: 5x³−21x²−21x+5 ≥0 ⇔ (x+1)(x−5)(5x−1)≥0

Perpetuo: a możesz mi rozpisać jak Ci wyszły te x wszystkie ? Bo niestety z tym mam problem

Eta: W(−1)=0 ⇒ x=−1 jest pierwiastkiem wielomianu W(x) lewej strony nierówności z dzielenia Hornerem przez (x+1) 5 −21 −21 +5 −1 − 5 26 −5 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 5 −26 5 0

	1
(x+1)(5x2−26x+5) , Δ= 576 x= 5 v x=
	5

	1
miejsca zerowe x= −1 v x=5 v x=
	5

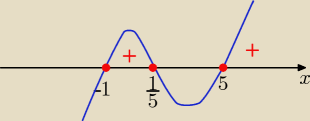
i wykres "fala" .........

Perpetuo: dzięki wielkie

Eta: 2 sposób Z rozkładu na czynniki 5x³+5 −21x²−21x = 5(x³+1)−21x(x+1) ( ze wzoru a³+b³=(a+b)(a²−ab+b²) = 5(x+1)(x²−x+1)−21x(x+1)= (x+1)(5x²−5x+5 −21x)= (x+1)(5x²−26x+5)

Perpetuo: właśnie próbowałam tym drugim sposobem i mi nie wychodziło ale dzięki