 To zacznijmy od pierwszego najłatwiejszego, granice całkowania masz ładnie określone teraz
tylko zostało stwierdzić, która powierzchnia jest wyżej, z = xy, czy z = 0 dla danych naszych
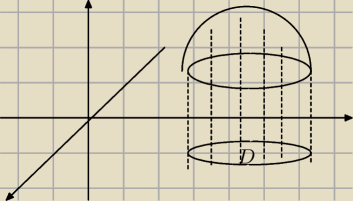
przedziałów. A jaka w ogóle jest interpretacja geometryczna takiej całki podwójnej (rysunek)
To co na rysunku to jakiś płat, kawałek powierzchni dla określonych x i y i całka :
V = ∫∫D f(x,y) dx dy
To nasza objętość! Jest to analogiczna interpretacja jak przy całce pojedynczej tylko to była
powierzchnia pod nią. bardziej ogólnie dla tej całki podwójnej to dodajemy kolejny płat/
płaszczyznę i taka objętość pomiędzy tymi płaszczyznami będzie równa :
V = ∫∫D (f(x,y) − g(x,y)) dx dy
Jak widać trzeba określić, która jest wyżej, a która niżej. Tak samo mieliśmy z całką
pojednczą, z tymże liczyliśmy pole między krzywymi, w praktyce wiedza czy coś jest wyżej czy
niżej niekoniecznie jest przydatna, bo gdy wyjdzie nawet wynik ujemny, można wziąć wartość
bezwzględną i wynik się elegancko zgozi.
Tyle tytułem wstępu. Więc pytanie do Cb, jak będzie więc wyglądała Twoja całka już iterowana
(czyli rozbita na 2 pojedyncze)
A i nie wspomniałem o zamianie całki podwójnej na iterowaną :
∫∫D f(x,y) dx dy = ∫ba dx ∫g(x)h(x) f(x,y) dy
Czyli nasze a,b to ograniczenie na osi iksów, nasze funkcje g(x) i h(x) to ograniczenie jakimś
krzywymi.
To zacznijmy od pierwszego najłatwiejszego, granice całkowania masz ładnie określone teraz
tylko zostało stwierdzić, która powierzchnia jest wyżej, z = xy, czy z = 0 dla danych naszych
przedziałów. A jaka w ogóle jest interpretacja geometryczna takiej całki podwójnej (rysunek)
To co na rysunku to jakiś płat, kawałek powierzchni dla określonych x i y i całka :
V = ∫∫D f(x,y) dx dy
To nasza objętość! Jest to analogiczna interpretacja jak przy całce pojedynczej tylko to była
powierzchnia pod nią. bardziej ogólnie dla tej całki podwójnej to dodajemy kolejny płat/
płaszczyznę i taka objętość pomiędzy tymi płaszczyznami będzie równa :
V = ∫∫D (f(x,y) − g(x,y)) dx dy
Jak widać trzeba określić, która jest wyżej, a która niżej. Tak samo mieliśmy z całką
pojednczą, z tymże liczyliśmy pole między krzywymi, w praktyce wiedza czy coś jest wyżej czy
niżej niekoniecznie jest przydatna, bo gdy wyjdzie nawet wynik ujemny, można wziąć wartość
bezwzględną i wynik się elegancko zgozi.
Tyle tytułem wstępu. Więc pytanie do Cb, jak będzie więc wyglądała Twoja całka już iterowana
(czyli rozbita na 2 pojedyncze)
A i nie wspomniałem o zamianie całki podwójnej na iterowaną :
∫∫D f(x,y) dx dy = ∫ba dx ∫g(x)h(x) f(x,y) dy
Czyli nasze a,b to ograniczenie na osi iksów, nasze funkcje g(x) i h(x) to ograniczenie jakimś
krzywymi.
| 1 | 1 | |||
V = ∫21 dx ∫10 (xy − 0) dy = ∫21 [ | xy2]10 dx = ∫21 | x dx = | ||
| 2 | 2 |
| 1 | 1 | 3 | ||||
= [ | x2]21 = 1 − | = | ||||
| 4 | 4 | 4 |