Geometria Michał: Wyznacz kąty czworokąta wpisanego w okrąg wiedząc, że przedłużenia boków AD i BC przecinają się pod kątem 30 zaś |∡A| : |∡B|=2:3( nie wiem czy użyłem poprawnego znaku, ale chodzi o miare konta).

Eta: Jakiego konta ? w PKO czy BGŻ ?

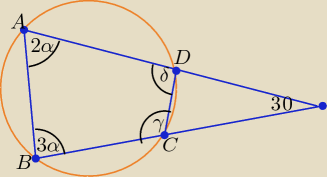
Bogdan: 2α + 3α + 30^o = ... ⇒ α = ... 2α + γ = ... 3α + δ = ...

pigor: ..., otóż z warunków zadania niech : |∡A|=2α i |∡B|=3α ⇒ 5α+30^o= 180^o ⇒ α= 30^o , więc |∡A|=2*30^o= 60^o i |∡B|=3*30^o= 90^o ⇒ |∡C|= 18^o−60^o= 120^o i |∡D|= 90^o − z tw. o sumie przeciwległych kątów czworokąta wpisanego w okrąg, a więc odp. Szukane kąty mają miary A=60^o , B=D=90^o , C=120^o . ...

pigor: ..., no to teraz Michał masz jak na tacy . ...

Eta: I ".... , otóż" pigor podał na złotej tacy rozwiązanie ( czyt. gotowca