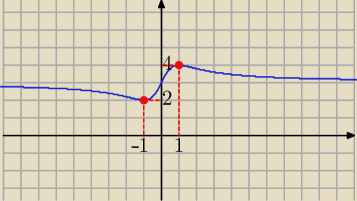
dowód na zbiór wartości funkcji krzysiek: Wykaż, że funkcja określona wzorem f(x) =^{3x2 + 2x + 3}_{x² + 1} , gdzie x ∊ R, przyjmuje najmniejszą wartość 2, zaś największą 4.

wredulus_pospolitus:

	1
zapisz jeszcze raz używając U (		) zamiast u (1√2)
	√2

wredulus_pospolitus: dodatkowo −−− liceum czy studia

krzysiek:

3x2 + 2x + 3
x2 + 1

Liceum dodatkowo powiem że nie miałem jeszcze delty

Eta: Przedszkole

krzysiek: Jak się dowiem jak to zrobić też się będę śmiał a tymczasem czekam na rozwiązanie ..

pigor: ..., np. tak :

	3x2+2x+3
y=		/ * (x2+1) >0 dla ∀x∊R ⇒ yx2+y−3x2−2x−3= 0 ⇔
	x2+1

⇔ (y−3)x²−2x+y−3= 0 i y≠1, to Δ ≥ 0 ⇔ 4−4(y−3)(y−3) ≥0 /:4 ⇔ 1−(y−3)² ≥ 0 ⇔ ⇔ (y−3)²≤ 1 ⇔ |y−3| ≤ 1 ⇔ −1 ≤ y−3≤ 1 /+3 ⇔ 2 ≤ y≤ 4, czyli y∊[2;4] c.n.w.

krzysiek: Jeszcze raz powiem że nie miałem delty

Eta:

pigor: ., ja nienawidzę 'delty", ale to jest akurat ten przykład, do którego jest ona idealna, bo inna metoda elementarna jest, ale uciążliwa (nie mam na myśli pochodnej), a nie chce mi się nią bawić (szkoda mojego czasu), dlatego zapytam : a kto ci dał to zadanie , bo jeśli jesteś ... nadgorliwy i sam wybiegasz z materiałem do przodu, to po prostu zapoznaj się z Δ−tą sam, a jak nie, to po prostu jeszcze do tego zadania nie dorosłeś i tyle , amen .

Eta:

pigor: . ... śmiej się Eta, śmiej , no bo co, nie mam racji

Eta: Masz 100%%%%%%%%%%%

krzysiek: Zamiast sie rozpisywać wystarczy napisać "nie chce mi się" ale przecież najlepiej przypiąć kilka epitetów komuś innemu. Nie wybiegam z programem, dał mi je nauczyciel wraz z 2 setkami zadań które mogę mieć na sprawdzianie z całeogo roku powinieneś mi podziękować że dzięki mnie połechtałeś swoje EGO

pigor: ... i tu mnie wkur...eś , bo to ty właśnie masz to swoje EGO (bo ja mam tylko ego) za wysokie i powinieneś "całować" moje cztery litery za takie rozwiązanie, bo słowa dziękuję to ty nie znasz, tylko powiadasz " jeszcze raz powiem, że nie miałem delty'' tonem nie znoszącym sprzeciwu, dlatego olewam cię − delikatnie i z małej litery , bo właśnie na to zasługujesz kolego .

krzysiek: Tak ma pan rację panie pigor przepraszam pana że nie przeczytał pan wcześniejszego postu i że nie podziękowałem panu za rozwiązanie które nic mi nie mówi oraz za to że nie "miałem jeszcze delty" napewno się z nią zapoznam skoro tak PAN radzi

pigor: ..., no to może teraz, dla podwyższenia swojego, a obniżenia najjaśniejszego pana EGO, rzucę na pożarcie (grozi zadławieniem), coś takiego :

	3x2+2x+3		3x2+3+2x+3		3(x2+1)+2x		2x
f(x)=		=		=		= 3+
	x2+1		x2+1		x2+1		x2+1

	2x
i niech teraz f(x)= 3+y(*) , gdzie y=		⇔ yx2+y−2x= 0 / : y≠0
	x2+1

(patrz

	1		1		1
wzór f) ⇒ x2−2yx+1= 0 /+		−1 ⇔ x2− 2*1yx+		=		−1 ⇔
	y2		y2		y2

	1		1
⇔ (x−1y)2=		−1 i		−1 ≥ 0 / * y2 ⇔ 1−y2 ≥0 ⇔ y2 ≤ 1 ⇔
	y2		y2

⇔ |y| ≤ 1 ⇔ −1 ≤ y ≤ 1 /+3 , wtedy stąd i z (*) powyżej mamy ⇔ ⇔ −1+3 ≤ y+3 ≤ 1+3 ⇔ 2 ≤ f(x) ≤ 4 ⇔ f(x) ∊ [2 ; 4] c.n.w. . ...

krzysiek: Dziękuje bardzo, o to mi chodziło moje EGO leży w gruzach przed pańskimi obliczeniami

pigor: ..., nie jest tak źle; bo ważne jest to, że potrafiliśmy sobie . ... wybaczyć,a o to chodzi nie tylko na forum, bo przecież − jak mawiał klasyk − można różnić się pięknie, pozdrawiam