Wyznacz m zero, okresl D i Zw Jowajt: Narysuj wykres, wyznacz m zerowe, określ dziedzinę i zbiór wartości. y=^3x−2_x+1

wredulus_pospolitus: i problem polega na ....

Jowajt: na postaci kanonicznej, przepraszam, nie dopisałam. wychodzi mi ^3x+3_x+1−5 ale zapewne źle wychodzi znając mnie.

Beti:

	3x−2		3(x+1)−5		5		5
y =		=		= 3 −		= −		+ 3
	x+1		x+1		x+1		x+1

Eta:

	3(x+1)−5		5
y=		= 3−		, dla x ≠ −1
	x+1		x+1

Jowajt: Dziękuję

pigor: ..., otóż, robisz np. tak :

	3x−2
y=		i x+1≠0, czyli Df= R\{−1} − dziedzina danej funkcji
	x+1

dalej

	3x−2		3x+3−3−2		3(x+1)−5		5		5
y=		=		=		= 3 −		= −		+3 ,
	x+1		x+1		x+1		x+1		x+1

więc Zw.= <2;+∞} − zbiór wartości danej funkcji ; −−−−−−−−−−−−−−−−−−−

	−5
teraz rysujesz sobie przerywana linią wykres funkcji y=		i przesuwasz go
	x

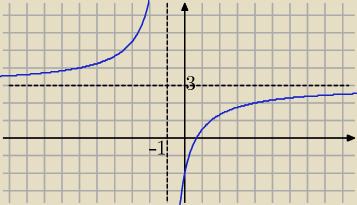
o wektor [−1,3] , czyli w lewo o 1 i do w góry o 3 jednostki i otrzymujesz szukany wykres (hiperbolę), dla którego prosta o równaniu x= −1 jest jego asymptotą pionową, a prosta y= 3 , jego asymptotą poziomą ....