Twierdzenie sinusów i cosinusów pedro: 1.W trójkącie ABC są dane AC= 2, CB= 4 , ∢BAC = 30°. Oblicz długość trzeciego boku tego trójkąta oraz promień okręgu opisanego 2. W trójkącie dane są długości boków 6dm, 4dm, 50 cm. Roztrzygnij, czy jest to trójkąt ostrokątny czy rozwartykątny (samo słownie to za malo) dzięki za pomoc

wredulus_pospolitus: 1. tw. cosinusów

wredulus_pospolitus: 2. zamień na jednakowe jednostki 'oszacuj' wartość cosinusa dla każdego z kątów (tw. cosinusów)

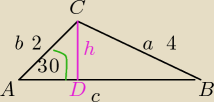
Mila: z tw. sinusów:

a		4
	=2R ⇔		=2R
sin30		0,5

2R=8 R=4 − dł. promienia okręgu opisanego na ΔABC W ΔADC:

	AD		√3
cos 30=		⇔AD=2*cos30=2*		⇔|AD|=√3
	2		2

	h
sin30=		⇔h=1
	2

W Δ CDB: 4²=1²+DB² 15=DB² |DB|=√15 |AB|=√3+√15

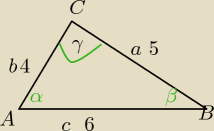
Mila: zadanie 2. W trójkącie dane są długości boków 6dm, 4dm, 50 cm. Roztrzygnij, czy jest to trójkąt ostrokątny czy rozwartokątny. 6dm,4dm, 5dm Jeżeli trójkąt jest rozwartokątny to cos|∡ACB|<0 ( naprzeciw najdłuższego boku leży największy kąt) Z tw. cosinusów: 6²=4²+5²−2*4*5 cosγ ⇔ 36=16+25−80cosγ 36=41−80cosγ −5=−80cosγ

	5
cosγ=		>0 zatem ΔABC jest ostrokątny
	80

Eta: a²+b²=c² −−− trójkąt prostokątny a²+b²>c² −−− trójkąt ostrokątny a²+b²< c² −−− trójkąt rozwartokątny a=4, b= 5 , c= 6 4²+5²= 16+25= 41 , c²=6²=36 zatem a²+b²>c² −−− trójkąt jest ostrokątny

pedro: dzięki wszystkim za pomoc

Mila: