 gdzie robię błąd?
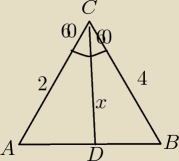
W trójkącie ABC dane są |BC| = 4cm , |AC|=2cm, |∡ACB| = 120. Wyznacz długość odcinka
dwusiecznej kąta ACB, zawartego w tym trójkącie
|AB| = c
c2 = 4 + 16 + 8*12
c2 = 28, c = 2√7
z tw. o dwusiecznej w trójkącie:
gdzie robię błąd?
W trójkącie ABC dane są |BC| = 4cm , |AC|=2cm, |∡ACB| = 120. Wyznacz długość odcinka
dwusiecznej kąta ACB, zawartego w tym trójkącie
|AB| = c
c2 = 4 + 16 + 8*12
c2 = 28, c = 2√7
z tw. o dwusiecznej w trójkącie:
| |AD| | DB | ||
= | |||
| 2 | 4 |
| 4√7 | 2√7 | |||
|DB| = | , |AD| = | |||
| 3 | 3 |
| 16*7 | |
= 16 + x2 −4x | |
| 3 |


| 1 | √3 | |||
PΔABC= | *2*4 sin(1200)=4*sin(180−60)=4* | |||
| 2 | 2 |
| 1 | 1 | √3 | √3 | |||||
PΔABC= | *2*d sin60+ | *4*d sin60=d* | +2d * | |||||
| 2 | 2 | 2 | 2 |
| √3 | 3√3 | |||
PΔABC=d*( | +√3)= | d⇔ | ||
| 2 | 2 |
| 3√3 | |
d=2√3⇔ | |
| 2 |
| 3 | 2 | ||
d=2 /* | |||
| 2 | 3 |
| 4 | ||
d= | ||
| 3 |
| 4√7 | 16*7 | |||
DB2=( | )2= | |||
| 3 | 9 |