Pilot helikoptera lecącego na wysokości 500m n.p.m. zauważył żaglówkę.... jaaaaa: Pilot helikoptera lecącego na wysokości 500m n.p.m. zauważył żaglówkę pod kątem depresji 15°. Oblicz odległość helikoptera od żaglówki. Wynik zaokrąglij do 1m.

Radek: Mam pytanie odnośnie tego zadania. Jeżeli wiem że jedna z przyprostokątnych to 500, a x oznaczam drugą przyprostokątną, a y to przeciwprostokątna to mam teraz obliczyć cosinusa 15 stopni.

	500
cos15=
	y

	500
0,9659=
	y

0,9659y=500 y=517,65m To jeżeli znam jeną przyprostokątną 500 i przeciwprostokątna 517 to z pitagorasa mam obliczyć x i to będzie ta odległość ?

Radek: Wie ktoś może ?

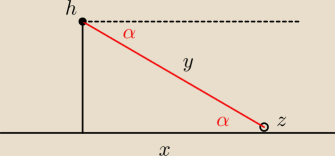
MQ: Moim zdanie to y jest odległością do żaglówki.

	500
Poza tym		=sin 15o, a nie cosinus.
	y

Radek: No właśnie ja nie wiem czy x czy y jest tą odległością

	0.5
To jeżeli tak jak piszesz to cos15=		?
	y

MQ:

	x
cos 15o=
	y

Radek: A czemu 15 stopni zaznaczamy przy alpha ? a nie przy h ?

MQ: α −− kąt depresji −− kąt poniżej horyzontu