pole Grzesiek: pole oblicz pole okreslone wykresami y=x i y=−x²+2x

Grzesiek: i drugie zadanie obliczyc całkę x ≥ 0 ʃʃ_D(x+y+1)dxdy gdzie D= y ≤ y ≤ −x+2 tylko dziedziny nie mam jeszcze pelnej

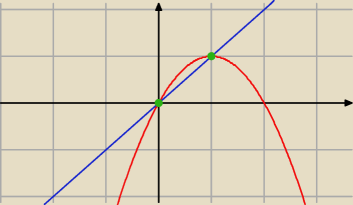
jikA: y = x ∧ y = −x² + 2x −x² + 2x = x x² − x = 0 x(x − 1) = 0 ⇒ x = 1 ∨ x = 0

	1		1
∫10 (−x2 + 2x − x)dx = ∫10(−x2 + x)dx = [−		x3 +		x2]10 =
	3		2

	1		1		1
−		+		=		.
	3		2		6

jikA: To napisz tą dziedzinę.

Grzesiek: tylko nie wiem jaka bo mi nie napisala a ja nie widze

Grzesiek: macko nie wiem co tam jest

jikA: Niech Ci napisze i będzie spokój.

Grzesiek: wlasnie cos mi nie odpisuje...

Grzesiek: jeszcze jest do policzenia dlugosc luku krzywej ale tez nie widze co tam jest...

Grzesiek: powiedzmy ze tam jest y< x moze tak byc

jikA: Może i może.

Grzesiek: długosc luku krzywej x(t)=e^tsint y(t)=e^tcost dziedzina t = (0 , i nie wiem ile tu jest zaraz dopiesze)

Grzesiek: dziedzina t = (0, π/2)

Grzesiek: robisz to obliczanie całki?

jikA: Robię.

Grzesiek: t2 __________ Długość krzywej L = ∫ √ (x')2 + (y')2 dt t1 jak sie to wrzuci do tego wolframa to policzy ta krzywa

jikA: Tylko trzeba umieć ją wpisać.

Grzesiek: no wlasnie a umiesz>

jikA: Nie mam pewności w 100% co do tego.

	1
D1 = ∫10 ∫2 − x x (x + y + 1)dxdy = ∫10 ([xy +		y2 + y]2 − x x)dx =
	2

	1		1		3
∫10 ∫ [x(2 − x) +		(2 − x)2 + 2 − x]dx = ∫10 (−		x2 − x + 4 −		x2 −
	2		2		2

x)dx =

	2		2		7
∫10 (−2x2 − 2x + 4)dx = [−		x3 − x2 + 4]10 = −		− 1 + 4 =
	3		3		3

	1
D2 = ∫21 ∫x −x + 2(x + y + 1)dxdy = ∫21 ([xy +		y2 + y]x 2 − x)dx =
	2

	1		1
∫21 ([x2 +		x2 + x +		x2 + x − 4])dx = ∫21 (2x2 + 2x − 4)dx =
	2		2

	2		16		2		11
[		x3 + x2 − 4x]21 =		+ 4 − 8 −		− 1 + 4 =
	3		3		3		3

	11		7		18
D1 + D2 =		+		=		= 6.
	3		3		3

Grzesiek: a to z lukiem wpiszez w wolfram

jikA: x(t)=etsin(t) ⇒ x'(t) = et[sin(t) + cos(t)] ⇒ [x'(t)]2 = e2t[1 + 2sin(2t)] y(t)=etcos(t) ⇒ y'(t) = et[cos(t) − sin(t)] ⇒ [y'(t)]2 = e2t[1 − 2sin(2t)] ∫π/20 √e2t[1 + 2sin(2t)] + e2t[1 − 2sin(2t)]dt = ∫π/20 √2e2tdt = ∫π/20 √2etdt = [√2et]π/20 = √2 * eπ/2 − √2.