zle licze calkeeeee. slawomir: Objetosc, calk podwojna. Witam! Mam do policzenia całkę: x² + y² = z² , x² + y² = 2y... I tak: wyszedł mi obszar normalny: 0 < r < 2sint 0 < t < 2π a całka po ktorej licze to ∫(od 0 − 2π)∫(od 0 do 2sint) (2√x² + y²) − podstawiam za x = rcost za y = rsint , domnazam przez jakobian, licze i wychodzi mi 0.... a nie taki jest wynik... Co robie zle? Pozdrawiam!

slawomir: spojrzy ktos?

Vizer: Jaką masz dokładną treść tego zadania, masz podane z czego całkujesz, czy masz policzyć objętość bryły ograniczonej tymi krzywymi co podałeś?

slawomir: mam obliczyc objetosc, jak sie domyslasz

slawomir: http://ifotos.pl/zobacz/201302041_nxrsxwq.jpg/ tu sa moje dokladne obliczenia

slawomir: popatrzycie?

slawomir: prosze serdecznie o pomoc...

slawomir: prosze o pomoc...

Vizer:

	64
Czy wynik to		?
	9

slawomir: tak, dokladnie

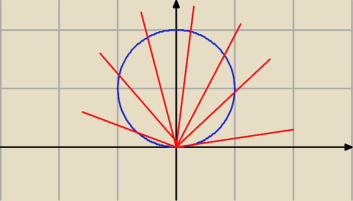
Vizer: Wziąłeś złą granicę całkowania przy φ, bo φ się zmienia od 0 do π, od od 0 do 2π miałbyś wtedy gdyby okrąg miał środek w (0,0). Dla zilustrowania zrobię rysunek. Ewentualnie mógłbys mieć takie granice całkowania : 0 ≤ φ ≤ 2π 0 ≤ r ≤ 1 Ale to jest przy zmienionym układzie współrzędnym tak by środek tego okregu był jakby w (0,0), żeby takie coś uzyskać trzeba podstawić takie współrzędne biegunowe : x = rcosφ y = rsinφ + 1 Tylko wtedy funkcja podcałkowa może być gorsza do policzenia, ale nie sprawdzałem.

slawomir: Vizer i wlasnie tych granic calkowania w okregach ja nie rozumiem. wiem jak rozpisac to co ogranicza r. ale to co ogranicza fi, zawsze sie myle. Chyba nie bardzo rozumiem jak to dziala. Czy moglbys mi to wytlumaczyc?

slawomir: zawsze myle sie jak okrag jest przesuniety. bo jak jest na srodku to zawsze jest od 0 do 2π

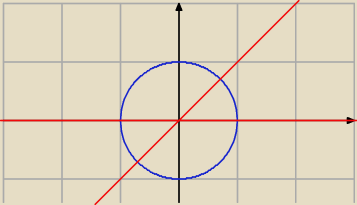
Vizer: Jak jest na środku i nic go nie ogranicza to jest od 0 do 2π. Powiedz mi jak sie będzie zmieniać φ dla okręgu ograniczonego przez prostą y = x i y = 0? (rysunek)

slaw: −3/4π − π/4, ?

Vizer: Chodziło mi o obszar w pierwszej ćwiartce więc jeszcze warunek x ≥ 0. A to co napisałeś to nie wiem czego się może tyczyć.

slaw: aha, zapomnialem o y = 0 xD wiec jest to od 0 do π/4

Vizer: No dobrze. A zamiast y = 0 gdyby było x = 0?

slaw: − π/2 do π/4

Vizer:

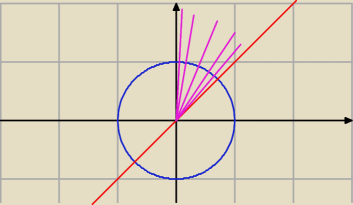
	π		π
No jak, powinno być od		do		, zawsze zaczynaj od prawej strony i patrz jaki kąt Ci
	4		2

wyjdzie do lewej strony aż do napotkania ogranicznika. Tutaj mamy tak (rysunek).

slaw: aha Bo ja patrzylem od dolu, co jest chyba bledem.

slaw: Mam jeszcze takie coś: x² + y² ≤ 6x oraz y ≥0 Obszar normalny ktory wyznaczylem to: 0 ≤ r ≤ 6cost 0 ≤ t ≤ π/2 tu tez gdzies jest chyba blad.... Tylko gdzie?

Vizer: Tu raczej błędu nie ma, a coś nie wychodzi?

slaw: tak mam po tym obszarze policzyc calke podwojna

	(x+y)2
∫∫		dxdy
	x2 + y2

ostatecznie wychodzi mi :

	9
9t +		sin(2t) − 9cos4t | na gorze (π/2) na dole 0
	2

i daje mi to: 9/2π + 9 a powinno byc poprostu 9π :(

slaw: zerknalbys na to?

Vizer: Tak wychodzi gdy nie ma założenia na y ≥ 0.

slaw: 9π wtedy wychodzi? To moze maja blad...

Vizer: Tak wtedy bierzesz pod uwagę też dolną część kołą i granice całkowania będą

	π		π
od −		do
	2		2