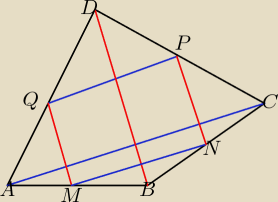
 na mocy twierdzenia odwrotnego do tw.Talesa
MN || AC i PQ || AC ⇒ MN || PQ
analogicznie
NP || BD i MQ || BD ⇒ NP || MQ
na mocy twierdzenia odwrotnego do tw.Talesa
MN || AC i PQ || AC ⇒ MN || PQ
analogicznie
NP || BD i MQ || BD ⇒ NP || MQ
| 1 | ||
PQ||AC i PQ= | AC | |
| 2 |
| 1 | ||
ΔPQD∼ΔACD w skali | ||
| 2 |
| 1 | ||
PΔPQD= | PΔACD | |
| 4 |
| 1 | ||
PΔMNB= | PΔACB | |
| 4 |
| 1 | ||
PΔPNC= | PΔDBC | |
| 4 |
| 1 | ||
PΔMQA= | PΔDBA | |
| 4 |
| 1 | ||
PMNPQ=PABCD− | (PΔACD +PΔACB+PΔDBC+PΔDBA)= | |
| 4 |
| 1 | 1 | |||
=PABCD− | *2PABCD= | PABCD | ||
| 4 | 2 |