Calka podwojna, obszar normalny. slawomir: Witam! Mam obliczyc całkę podwójną po obszarze ograniczonym: (x+1)² + (y−3)² ≤ 9, Czy dobrze okreslam obszar normalny we wsp biegunowych? D: { −1 ≤ r ≤2 , 0 ≤ t ≤ 2π} Pozdrawiam!

slawomir: cos mi sie wydaje ze zle, bo wychodzi mi zly wynik. Moze ktos mi rozpisac ten obszar? Ps. Nie nie zapominam o jakobianie xD

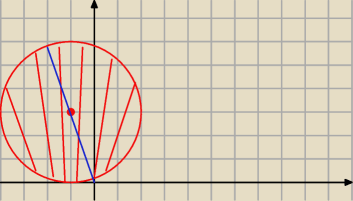
Basia: to jest Twój obszar D; to jak sądzisz ? to niebieskie to największe możliwe r, ile ma ? i od kiedy promień może być ujemny ? r ∊<0;6> a kąt ∊(0; π) ale nie korzystałabym tutaj ze współrzędnych biegunowych x∊<−4;2> y ∊< −a_x; a_x> gdzie a_x = √9−(x+1)² + 3 = √−x²−2x+10 + 3

slawomir: kurcze, troche to skomplikowane. A jakbym zapisal wtedy { 0 ≤ r ≤ 3 , 0 ≤ t ≤ 2π ? Uczepiłem sie tych biegunowych ale to zadanie napewno ma byc robione w biwgunowych. Bo to akurat ten rodzaj przykładów w ksiazce.

Basia: sorry błąd; y∊ < −√−x²−2x+10+3; √−x²−2x+10+3> ale jak mają być biegunowe to chyba trzeba rozważyć dwa oddzielne przedziały

Basia: tyle, że bez przechodzenia na biegunowe to całkiem proste całki podwójne