Geometria Okręgi D o w ó d
V.Abel:
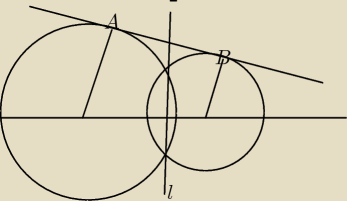
Cześć! Proszę o pomoc:
dane są dwa okręgi przecinające się o promieniach R
1 i R
2. środki tych okręgów leżą na jednej
prostej. Poprowadzono styczną do tych okręgów i poprowadzono promienie do punktu styczności.
Wykaż, że prosta l przechodząca przez przecięcia się okręgów dzieli odcinek AB na połowy,
gdzie odpowiednio A i B to punkty styczności, do których poprowadzono promień.
HELP

!
8 cze 17:35
Eta:
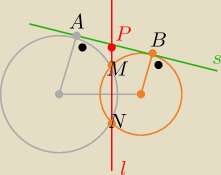
P€ pr . s −−− styczna do okręgów
i P€ l oraz M, N€ l i do okręgów l −−− jest sieczną okręgów
Skorzystaj dwa razy z tw. o stycznej i siecznej
( |AP|
2= |PM|*|PN| i |BP|
2= |PM|*|PN| ) ⇒|AP|=| PB|
zatem P jest środkiem odcinka AB
c.n.u
8 cze 17:58
Eta:
Dodaj eszcze dokończenie komentarzem:
P jest środkiem odcinka AB , to prosta "l" dzieli odcinek AB na połowy
8 cze 18:03
V.Abel: ahaaa dobrze mieć dobre pomysły, mega WIELKIE dzięki...

a tak gwoli ścisłości to jedyny sposób? ja sobie trójkąty dorysowywałem do to przecięcia
okręgów, to do punktu P ...
8 cze 18:12
Mila:
Na pewno nie jedyny, przecież udowodniono tw. o stycznej i siecznej, ale po co wyważać otwarte
drzwi?
8 cze 18:26
V.Abel:
bo ja zawsze szukam po tysiąc sposobów na to samo

może znajdę

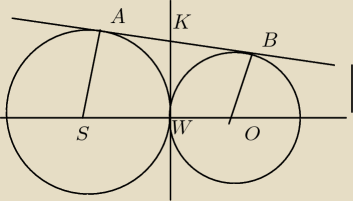
w takim razie prosiłbym o sprawdzenie zadania o takiej samej treści z tą różnicą, że okręgi są
styczne(w zadaniu były dwa podpuknty), ale wolę się upewnić, czy mam dobrze, a więc: doszedłem
do wniosku, że AKWS i KBOW to deltoidy i tyle, udowodnione, tylko, że ja napisałem tak:
ponieważ |SW|=|SA| oraz |WO|=|BO| i odcinki |AK|, |KB| leżą na jednej prostej to są to
deltoidy, ale nie jestem pewien czy to uzasadnienie rozwiewa wszelkie wątpliwości... co Wy na
to ? ..
8 cze 18:37
V.Abel: tego odcinka pionowego po prawej formalnie nie ma. nie "wyczyściłem"
8 cze 18:38
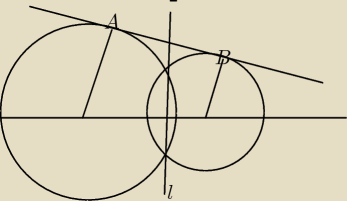 Cześć! Proszę o pomoc:
dane są dwa okręgi przecinające się o promieniach R1 i R2. środki tych okręgów leżą na jednej
prostej. Poprowadzono styczną do tych okręgów i poprowadzono promienie do punktu styczności.
Wykaż, że prosta l przechodząca przez przecięcia się okręgów dzieli odcinek AB na połowy,
gdzie odpowiednio A i B to punkty styczności, do których poprowadzono promień.
HELP
Cześć! Proszę o pomoc:
dane są dwa okręgi przecinające się o promieniach R1 i R2. środki tych okręgów leżą na jednej
prostej. Poprowadzono styczną do tych okręgów i poprowadzono promienie do punktu styczności.
Wykaż, że prosta l przechodząca przez przecięcia się okręgów dzieli odcinek AB na połowy,
gdzie odpowiednio A i B to punkty styczności, do których poprowadzono promień.
HELP !
!
 P€ pr . s −−− styczna do okręgów
i P€ l oraz M, N€ l i do okręgów l −−− jest sieczną okręgów
Skorzystaj dwa razy z tw. o stycznej i siecznej
( |AP|2= |PM|*|PN| i |BP|2= |PM|*|PN| ) ⇒|AP|=| PB|
zatem P jest środkiem odcinka AB
c.n.u
P€ pr . s −−− styczna do okręgów
i P€ l oraz M, N€ l i do okręgów l −−− jest sieczną okręgów
Skorzystaj dwa razy z tw. o stycznej i siecznej
( |AP|2= |PM|*|PN| i |BP|2= |PM|*|PN| ) ⇒|AP|=| PB|
zatem P jest środkiem odcinka AB
c.n.u
 a tak gwoli ścisłości to jedyny sposób? ja sobie trójkąty dorysowywałem do to przecięcia
okręgów, to do punktu P ...
a tak gwoli ścisłości to jedyny sposób? ja sobie trójkąty dorysowywałem do to przecięcia
okręgów, to do punktu P ...
 bo ja zawsze szukam po tysiąc sposobów na to samo
bo ja zawsze szukam po tysiąc sposobów na to samo  może znajdę
może znajdę  w takim razie prosiłbym o sprawdzenie zadania o takiej samej treści z tą różnicą, że okręgi są
styczne(w zadaniu były dwa podpuknty), ale wolę się upewnić, czy mam dobrze, a więc: doszedłem
do wniosku, że AKWS i KBOW to deltoidy i tyle, udowodnione, tylko, że ja napisałem tak:
ponieważ |SW|=|SA| oraz |WO|=|BO| i odcinki |AK|, |KB| leżą na jednej prostej to są to
deltoidy, ale nie jestem pewien czy to uzasadnienie rozwiewa wszelkie wątpliwości... co Wy na
to ? ..
w takim razie prosiłbym o sprawdzenie zadania o takiej samej treści z tą różnicą, że okręgi są
styczne(w zadaniu były dwa podpuknty), ale wolę się upewnić, czy mam dobrze, a więc: doszedłem
do wniosku, że AKWS i KBOW to deltoidy i tyle, udowodnione, tylko, że ja napisałem tak:
ponieważ |SW|=|SA| oraz |WO|=|BO| i odcinki |AK|, |KB| leżą na jednej prostej to są to
deltoidy, ale nie jestem pewien czy to uzasadnienie rozwiewa wszelkie wątpliwości... co Wy na
to ? ..