Pomocy ewelina: muszę na jutro(zaoczne) oddać wyznaczony przebieg zmienności funkcji. nie mam pojęcia jak to zrobić.poprosiła bym o komentarz, bo muszę opowiedzieć dlaczego jest tak a nie inaczej. oto moja funkcja: y=excosx Mógłby ktoś to rozwiązać, nie musi to być ładnie schludnie, byle wyniki były.

wredulus_pospolitus: nie wiesz jak to już piszę: 1) wyznacz dziedzinę funkcji 2) wyznacz przecięcia z osiami OX (miejsca zerowe) i OY 3) sprawdź czy funkcja jest parzysta/nieparzysta 4) wyznacz granice w +/−∞ oraz w punktach wykluczonych z dziedzin (jeżeli takie istnieją) 5) wyznacz asymptoty w tych punktach jak również sprawdź czy istnieją asymptoty w krańcach ... czyli w +/−∞ (asymptota może być tam ukośna lub jej uproszczona wersja czyli pozioma) 6) oblicz pochodną 7) przyrównaj pochodną do 0 8) rozwiąż to równanie ... wyznacz miejsca zerowe ... naszkicuj wykres tejże pochodnej 9) na podstawie tegoż szkicu podaj przedziały monotoniczności funkcji f(x) jak wskaż ekstrema i określ ich rodzaje 10) policz pochodną 2 rzędu 11) przyrównaj ją do 0 12) rozwiąż to równanie ... wyznacz miejsca zerowe ... naszkicuj wykres tejże drugiej pochodnej 13) na podstawie tegoż szkicu podaj przedziały wklęsłości/wypukłości funkcji f(x) jak wskaż punkty przegięcia 14) wyznacz wartości funkcji w punktach ekstremalnych jak również w punktach przegięcia 15) kooooniec A rozwiązać to Ty sama rozwiążesz ... zapiszesz je tutaj to sprawdzimy ... naprowadzimy ... nie ma tak łatwo

use: Brawo wredulus a jeżeli nie dasz rady, to widocznie nie potrzebny jest Polsce taki magister co "nie wiem " "nie umie " Chcę ,więc mogę, tego się trzymaj Powodzenia ^^

ewelina: jest jedna granica prawostrona, dziedzina to R ,miejsca zerowe x= pi*n− pi/2 y=0. pochodna e^x(sinx+cosx) do 0 pi*n−4/pi 2 pochodna 2e^xcosx do 0 pi*n−2/pi mógłby ktoś to potwierdzić lub wskazać błąd? najgorzej jest z asymptotami,nie dam rady wyliczyc ich, przy tym potrzebowałabym pomocy.moglibyście wyliczyc ją dla podstawowej wersji?

wredulus_pospolitus: druga pochodna mi się nie podoba 1 pochodna ok 2 pochodna ok miejsca zerowe pochodnych −−− też raczej ok asymptoty jeżeli istnieje granica (skończona) lim_x−>+∞ f(x) to jest w +∞ asymptota pozioma (i granica ją wyznacza) ... analogicznie dla −∞ jeżeli nie ... to sprawdzasz czy nie ma ukośnej liczysz:

	f(x)
limx−>+∞		... jeżeli ta granica jest skończona to masz pierwszy etap za sobą
	x

(wartość tej granicy oznaczasz jako 'a') liczysz teraz lim_x−>+∞ ( f(x) − a*x) ... jeżeli ta granica skończona to istnieje ukośna i jest ona dana wzorem y = a*x + b ... (gdzie 'a' to wynik pierwszej z tych granic ... a 'b' to wynik drugiej z nich)

wredulus_pospolitus: oś OY nie jest przecinana w punkcie (0,0) tylko w punkcie (0,1) (e⁰*cos0 = 1*1 = 1)

wredulus_pospolitus: jeżeli chociaż jedna z tych granic (asymptota ukośna) wyjdzie niewłaściwa (+/− ∞) natychmiast kończysz wyliczanie i piszesz ... brak asymptoty ukośnej w +∞ (analogicznie dla −∞)

ewelina: napisałam że dla OY jest y=1 a przy ox x=... co do asymptot po czym stwierdzic że np pionowa lewa nie istnieje? jeżeli granica lewostrona tak jak tu nie istnieje to nie ma też asymptoty z tej strony,dobrze zrozumiałam? sprawdź też czy dobrze mi wyszło że granicy z lewej strony nie ma.jak byś mógł to wstaw całe równanie tej lewostronnej granicy z którego wynika że jej brak,chciałabym się upewnić że np. mimo dobrego wyniku nie mam gdzieś błędu w obliczeniach.

ewelina: a widzę w OY gafe nie to wpisalam przy wprowadzeniu wyników, przepraszam

wredulus_pospolitus: pionowe MOGĄ być jeżeli dziedziną nie jest R asymptoty pionowa nie będzie istniała jeżeli granica dążąca do punktu 'wyjętego' z dziedziny nie będzie wynosić +/−∞ np. f(x) = x dla x>0 x+1 dla x<0 nie posiada asymptoty pionowej w x=0 ... ponieważ obie granice jednostronne w tym punkcie są skończone

wredulus_pospolitus: granica tej funkcji (Twojej) w −∞ istnieje i wynosi ona 0 lim f(x) = [(e^−∞*cos(−∞))] −> 0*(funkcja ograniczona) −> na mocy tw. o granicy trzech ciągów (trzech funkcji) −> =0 natomiast w +∞ nie istnieje granica

ewelina: więc tutaj asymptoty powinnam liczyć w skrajnych granicy +− nieskończoność, prawa lewa od 0, i to samo w 2 pochodnych granice +− nieskończoność i prawa lewa od ich miejsc zerowych, łącznie 12 asymptot? czy coś podkreślam?

wredulus_pospolitus: pokręciłaś D_f = R <−−− brak wywalanych punktów −> brak asymptoty pionowej jedyne asymptoty jakie mogą być to ukośne lub poziome ... czyli w +/−∞ (w −∞ będzie pozioma ... w +∞ brak asymptoty)

ewelina: i jak mam zapisać gdy w granicy mam sprzecznosc więc nie istnieje, kreska i dopisek brak granicy?

wredulus_pospolitus: jesteś studentką ... musisz 'wykazać' że granica nie istnieje tw. granica funkcji f(x) dla x−> +/−∞ istnieje wtedy i tylko wtedy gdy dla dowolnego ciągu {x_n} −> +/−∞ istnieje granica lim_n−>∞ f(x_n) (trochę przerobione tw. Heinego znane z granic ciągów) czyli ... wybierasz dwa 'podciągi' (x_n = 2nπ oraz x_k = 2kπ + π <−−− czyli w jednym cos x_n = 1 w drugim cos x_k = −1) i wykazujesz, że granice tych podciągów nie są sobie równe ... wniosek ... granica nieistnieje

ewelina: jestem z dmieszana na 102. powiedz mi dla dokładnie których punktów mam w całym zadaniu liczyć granice i asymtoty,np. druga pochodna granice +− nieskończoność asymptoty tu i tu. może tak zrozumiem.

ewelina: *zmieszana

wredulus_pospolitus: w pochodnych nie liczy się granic ... granice się liczy tylko z funkcji f(x) i tylko po to by wyznaczyć asymptoty dla tej funkcji

ewelina: podsumowując w podstawowej liczę 2 granice(+−nieskończoność) i jeśli są to 2 asymptoty ukosne w 1 pochodnej jeśli były granice w podstawowej to liczę 2 asymptoty ukosne (+−nieskończoność) w 2 pochodnej jak w pierwszej robię. teraz jest dobrze?

wredulus_pospolitus: pochodne wyznaczasz i przyrównujesz do 0 ponieważ z nich wyciągasz: a) kiedy f(x) jest rosnąca a kiedy malejąca (korelacja ze znakiem pochodnej w danym przedziale) b) gdzie funkcja f(x) posiada ekstremum (korelacja z miejscami zerowymi pochodnej) c) kiedy f(x) jest wklęsła/wypukła (korelacja ze znakiem drugiej pochodnej w danym przedziale) d) gdzie f(x) posiada punkty przegięcia (korelacja z miejscami zerowymi drugiej pochodnej) pamiętaj −−− nie każde miejsce zerowe pierwszej pochodnej oznacza, że tam f(x) posiada ekstremum

wredulus_pospolitus: może inaczej ... zrobię pełną wersję tego zadania ... ale dla jakiejś innej funkcji ... okey

wredulus_pospolitus: będzie to 'prosta funkcja' (z głowy daję):

	x3
f(x) =
	x2−1

możesz robić równolegle ze mną i sprawdzać później czy wychodzi to samo

wredulus_pospolitus: 1) D_f = R/{−1 , 1} (bo x²−1 ≠ 0 <=> x≠−1 i x≠1)

	x3
2) miejsce zerowe: 0 =		−> x = 0 ... od razu mamy ... przecięcie z osią OY dla
	x2−1

y=0 3) celowo 'oleję' parzystość/nieparzystość (chociaż ta funkcja akurat jest nieparzysta ... ta informacja jest bardzo pomocna ... bo w ten sposób połowę obliczeń można 'zlekceważyć')

ewelina: to lepiej.daj coś z analogicznym e^x * coś ale nie cosx

ewelina: ok robię równolegle

wredulus_pospolitus: 4) asymptota pionowa: w x=−1

	−1−		1
limx−>−1− f(x) = [		] = [		= −∞ (czyli już na pewno jest w
	(1+) − 1		0−

x=−1 asymptota pionowa ...przynajmniej lewostronna)

	−1+		−1
limx−>−1+ f(x) = [		] = [		= +∞
	(1−) − 1		0−

w x=1

	1−		1
limx−>1− f(x) = [		] = [		= −∞ (czyli już na pewno jest w x=−1
	(1−) − 1		0−

asymptota pionowa ...przynajmniej lewostronna)

	1+		1
limx−>1+ f(x) = [		] = [		= +∞
	(1+) − 1		0+

czyli istnieją dwie asymptoty pionowe ... w x=−1 oraz x=1

ewelina: a dlaczego dla +− nieskończoność nie liczysz granic?

wredulus_pospolitus: 4 cd) asymptota pozioma

	x3		x
limx−>+∞ f(x) = lim		= lim		= +∞ <−−− brak asymptoty poziomej
	x2−1		1 − 1/x2

badam ukośną

	f(x)		x3		x3		1
limx−>+∞		= lim		= lim		= lim		=
	x		(x2−1)*x		x3−x		1 − x/(x3)

	1		1
lim		=		= 1 <−−− czyli a=1
	1− 1/x2		1 − 0

	x3		x3 − x*(x2−1)
limx−>+∞ ( f(x) − a*x) = lim (		− 1*x) = lim		= lim
	x2−1		x2−1

	1
		= 0
	x2−1

<−−− czyli b=0 brak asymptoty poziomej w +∞ istnieje asymptota ukośna w +∞ i jest ona dana wzorem: y = 1*x + 0 ... czyli y=x analogicznie w −∞ (leń jestem ... sama możesz przeliczyć ... i napisz jakie granice Ci wyszły i jaki wzór ukośnej wyszedł)

wredulus_pospolitus: 5) pochodna

	3x2*(x2−1) − x3*2x		3x4 − 3x2 − 2x4
f'(x) =		=		=
	(x2−1)2		(x2−1)2

	x4−3x2
	(x2−1)2

D_f' = D_f = R/{−1,1} i teraz ważny 'myczek' ... jeżeli pochodna wychodzi w formie ułamka NIGDY nie skracasz licznika z mianownikiem ... ponieważ teraz: Dla każdego x∊D_f' (x²−1)² > 0 miejsca zerowe:

x4−3x2
	= 0 <=> x4 − 3x2 = 0 <=> x2(x2−3) = 0 <=> x2(x−√3)(x+√3) = 0
(x2−1)2

mamy trzy miejsca zerowe (0, √3 i −√3) w tym momencie możemy wykonać szkic wykresu pochodnej (i tu właśnie korzystamy z wcześniej zaznaczonego 'myczku' ... czyli informacji, że znak pochodnej zależy jedynie od jej mianownika ) //wykres w następnym poście//

ewelina: pozioma − nieskończoność. a więc brak ukosna tutaj pochodna bo wychodzi 2/0 więc metoda de hopitala (coś w nazwie pokrece) i jest: a=−1 b=0 więc y=−x

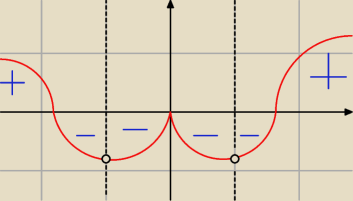
wredulus_pospolitus: czy wiesz dlaczego właśnie tak to wygląda

wredulus_pospolitus: uwaga do ukośnej

	f(x)
pokaż jak liczyłaś granicę z
	x

wredulus_pospolitus: 9) funkcja f(x) ↗ w (−∞,−√3); w (√3, +∞) funkcja f(x) ↘ w (−√3, −1); w (−1, 0); w (0,1); w (1, √3) funkcja posiada dwa ekstrema: maksimum dla x=−√3 minimum dla x=√3 i teraz pytania: a) czy wiesz dlaczego tak wyznaczałem przedziały gdzie funkcja maleje i dlaczego mam 'w' a nie znak sumy przedziałów ? b) czy wiesz dlaczego te ekstrema to maksima/minima i dlaczego w x=0 NIE MA ekstremum ?

ewelina:

x3
	=11−1=10 i stosuje regule biorę pochodne
x3−x

^2x2_2x²−1=¹_1−1/2x²=0.5 co liczę to inny wynik

wredulus_pospolitus: bzduuuura

	x3		x3*(1)		1
lim		= lim		= lim		= 1
	x3 − x		x3(1 − 1/x3)		1 − 1/x3

wredulus_pospolitus:

	1
ponieważ limx−>−∞		= 0
	x3

ewelina: a) nie b) bo to miejsce zerowe pochodnej

wredulus_pospolitus: a) bo gdybym zapisał, że maleje w przedziale (−√3,−1)u(−1,0) ... to by oznaczało, że dla dowolnych x₁ i x₂ w tej sumie przedziału .. jeżeli zachodzi x₁>x₂ to f(x₁)<f(x₂) ... ale ta funkcja nie jest CIĄGŁA więc nie musi to zachodzić (i nie zachodzi co możesz zauważyć tutaj: http://www.wolframalpha.com/input/?i=plot+%28x%5E3%2F%28x%5E2-1%29%29)

wredulus_pospolitus: b) i co z tego x=−√3 i x=√3 to także miejsca zerowe pochodnej ... tak samo jak x=0 ale czymś się one muszą różnić od siebie ... skoro wiem że w x=0 na pewno NIE BĘDZIE ekstremum (baaa ... wiem że będzie punkt przegięcia)

ewelina: moglibyśmy analogicznie zrobić właściwy przykład? boję się że go nie zrobię sama do jutra =(. zadam ci pytania do tego co niezrozumiem i jutro po zajęciach zrobię tu sAma jakiś przykład od ciebie(ok.16).zgodził byś na taki układ?

wredulus_pospolitus: pffff .... ale to jest tyyyyle roboty ojjj coś czuję że jedno piwo to będzie za mało

ewelina: jeśli pasują ci miejscowości to nie ma problemu=). przez pocztę to listonosz wypije i nic nie dotrze=)

ewelina: a dlaczego nie liczyłeś w tamtym przykładzie pochodnej 2 stopnia?

wredulus_pospolitus: f(x) = e^x*cosx D_f = R miejsce zerowe x=kπ przecięcie z osią OY: y=1 brak asymptoty pionowej (patrz dziedzina = R) sprawdzam czy istnieje asymptota pozioma w x=−∞ zauważam, że: e^x*(−1) ≤ e^x*cosx ≤ e^x*1 czyli zachodzi: lim_x−>−∞ e^x*(−1) ≤ lim_x−>−∞ e^x*cosx ≤ lim_x−>−∞ e^x*(1) lim_x−>−∞ e^x*(−1) = 0 lim_x−>−∞ e^x*(1) = 0 w takim razie lim_x−>−∞ e^x*cosx = 0 istnieje asymptota pozioma w −∞ (to należy jakoś 'ładniej' zapisać) sprawdzam czy istnieje asymptota pozioma w x=+∞ wprawionym okiem zauważam, że nie istnieje, a więc wypadałoby to udowodnić (tak jak napisałem ... wybacz ... ale nie mam siły tego pisać na portalu)

wredulus_pospolitus: tam nie policzyłem ... bo 'nie doszliśmy' do drugiej pochodnej

wredulus_pospolitus: liczymy 1 pochodną f'(x) = e^x(cosx−sinx) <−−− miałaś wcześniej źle wyliczoną pochodną

	π
ex(cosx−sinx) = 0 <=> ex = 0 lub cosx−sinx = 0 <=> cosx=sinx <=> x =		+kπ
	4

i teraz wypadałoby zrobić szkic wykresu pochodnej

ewelina: nie masz błędu w OX ? k*pi − pi/2 mi wychodzi

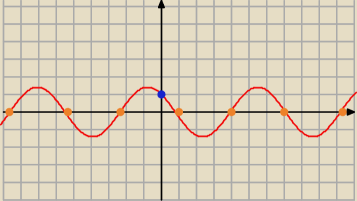
wredulus_pospolitus: jako, że jest nieskończenie wiele miejsc zerowych w tej pochodnej ... to nie można 'standardowo' szkicować (od prawej strony i lecimy do największego miejsca zerowego) zamiast tego ... wybieramy jakąś wartość (np. x=0) i sprawdzamy czy wartość pochodnej w niej będzie dodatnia czy ujemna (będzie dodatnia) ... i tej wartości robimy wężyka na lewo od x=0 ... oraz na prawo od x=0 ... stosując się do zasady, miejsce zerowe stopnia nieparzystego −> wykres 'przebija się' , miejsce zerowe parzystego stopnia −> wykres 'odbija się od osi OX' i w ten sposób powstaje powyższy szkic

wredulus_pospolitus: masz rację ... pośpieszyłem się z tymi miejscami zerowymi (wziąłem sinx zamiast cosx)

ewelina: ok, co dalej?

wredulus_pospolitus: teraz na podstawie szkicu wykresu (pamiętaj ... to NIE JEST wykres pochodnej ... a jedynie szkic wykresu) wypisujesz przedziały (wypisujesz je po przecinku ... jak ja wcześniej) w których pochodna jest dodatnia (wtedy f(x) rośnie) a w jakich ujemna (wtedy f(x) maleje) zauważasz że wszystkie miejsca zerowe są nieparzystego stopnia −−−−−> stąd wiemy że są one ekstremami funkcji f(x) (miejsce zerowe pochodnej pierwszej MUSI być nieparzystego stopnia, aby to było ekstremum) odpowiednio wyznaczasz które z nich to maksima (zmiana znaku pochodnej z + na −), a które to minima (zmiana znaku pochodnej z − na +)

wredulus_pospolitus: i teraz druga pochodna f''(x) = e^xsinx + e^xcosx −e^xcosx −e^x*(−sinx) = 2e^xsinx przyrównujesz do zera ... wychodzi sinx=0 rysujesz g(x) = sinx wyznaczasz przedziały (tak samo wypisujesz jak wcześniej ... po przecinku ) kiedy f'' jest dodatnia a kiedy ujemna ... z nich wiesz kiedy f(x) jest wklęsła a kiedy wypukła (sprawdź w notatkach ... bo ja szczerze mówiąc ... nie pamiętam ) miejsca zerowe drugiej pochodnej są nieparzystego stopnia ... stąd wiadomo że wszystkie te punkty (i tylko te punkty) są punktami przegięcia funkcji f(x)

ewelina: ok

wredulus_pospolitus: i to już koniec zadania tak naprawdę szczerze mówiąc ... nie jest to 'typowe' zadanie z przebiegu zmienności funkcji ... bo posiada (jak sama zauważyłaś) parę 'pułapek' (jak nieistnienie granicy lub też problem z nieskończoną liczbą miejsc zerowych pochodnych)

ewelina: będę to robila z pomocą mathcada.dam radę. dzięki za pomoc.

wredulus_pospolitus: zapoznaj się też z mathematicą (wolframalpha.com)