 Znajdź objętość bryły ograniczonej płaszczyznami układu współrzędnych i powierzchniami
z=4x2+2y2+1, x+y−3=0
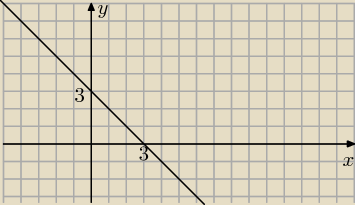
Wiem, że pierwsza powierzchnia to paraboloida podniesiona o 1 do góry, więc nie powinna wpłyać,
a nie zakłócać jakoś rzusu na oś OXY. Na płaszczyźnie z=0 obszar całkowania wyznaczają, więc
oś rzędnych i odciętych i prosta y=−x+3. Obszarem jest trójkąt.
x∊[0,3]
y∊[0,3−x]
A funkcją podcałkową powierzchnia z(x,y)=4x2+2y2+1.
Po iteryzacji całka więc wygląda tak:
Znajdź objętość bryły ograniczonej płaszczyznami układu współrzędnych i powierzchniami
z=4x2+2y2+1, x+y−3=0
Wiem, że pierwsza powierzchnia to paraboloida podniesiona o 1 do góry, więc nie powinna wpłyać,
a nie zakłócać jakoś rzusu na oś OXY. Na płaszczyźnie z=0 obszar całkowania wyznaczają, więc
oś rzędnych i odciętych i prosta y=−x+3. Obszarem jest trójkąt.
x∊[0,3]
y∊[0,3−x]
A funkcją podcałkową powierzchnia z(x,y)=4x2+2y2+1.
Po iteryzacji całka więc wygląda tak:
| 2 | ||
∫30 dx ∫03−x ((4x2+1)+2y2)dy=∫30 ((4x2+1)(3−x) + | (3−x)3 )dy=
| |
| 3 |
| 2 | 4 | 1 | ||||
∫30(12x2+3−4x3−x)dx− | ∫30(x−3)3dx=[4x3− | x5− | x2]20+6
| |||
| 3 | 5 | 2 |
| 2 | 1 | 128 | 1 | |||||
− | [ | (x−3)4]20=32− | −2+6− | =36−25−35−16= | ||||
| 3 | 4 | 5 | 6 |

| 4 | ||
Wychodzi 45, masz błędy rachunkowe tam nie powinno być | x5 po za tym górna granica jest | |
| 5 |
