pomocy siedem:

	x
POMOCY muszę obliczyć monotoniczność funkcji f(x) =
	x+1

ze wzoru x1 < x2 ⇒ f(x1) <f(x2)

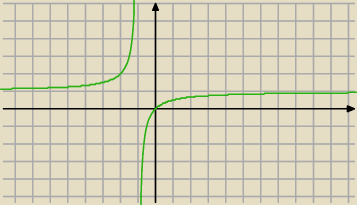
Technik: Myślę że to powinno Ci pomóc

siedem: tylko, że ja wiem ogólnie jak to zrobić, tylko że mam problem z ułamkiem , sprowadzam do wspólnego i nie wiem co dalej

Technik: pokaż jak robisz ?

asdf: no to pokaz gdzie masz problem, nie wpadles na to, ze jeszcze tego nie napisales?

siedem:

	x1		x2
T:		<
	1+x		1+x

po sprowadzeniu do wspólnego i redukcji zosatje mi

x1−x2
	< 0
(1+x1)(1+x2)

co dalej? Muszę udowodnic że funkcja jest rosnąca w przedziale x∊ (−∞, −1)

siedem: ehh, mała poprawka

	x1		x2
T:		<
	1+x1		1+x2

Technik: to widać z wykresu na to Ci go narysowałem

siedem: tak, ale ja mam to wykazać i to nie może być wykres tylko zapis

siedem: a mogę zrobić tak?

x1−x2
	<0 / pomnożyć stronami najpierw przez (1+x1) a potem (1+x2)
(1+x1)(1+x2)

zostanie x1 − x2 < 0, x1<x2

siedem: i w ten sposób otrzymuje założenie do twierdzenia

Vizer: No to widzisz, ze dla przedziału x∊(−∞, −1) mianownik będzie dodatni, co razem z dodatnim licznikiem daje wartość większą od zera.

Mila: Funkcja f(x) jest rosnąca w przedziałach: (−∞,−1) lub (−1,∞) 1) x₁,x₂∊(−∞,−1) i x₁<x₂⇔(x₁−x₂)<0 dla x∊(−∞,−1) wyrażenie x+1<0 Badamy znak różnicy: f(x₁)−f(x₂)

x1		x2		x1*(x2+1)−x2*(x1+1)
	−		=		=
x1+1		x2+1		(x1+1)(x2+1)

	x1*x2+x1−x2*x1−x2		x1−x2
=		=		<0 bo
	(x1+1)(x2+1)		(x1+1)(x2+1)

(x₁−x₂)<0 z założenia , (x₁+1)(x₂+1)>0 jako iloczyn dwóch liczb ujemnych. Zatem funkcja f(x) jest rosnąca w przedziale (−∞,−1) Podobnie dowód dla x∊(−1,∞)

Mila: Popełniasz błąd , dowodząc, że założenie jest prawdziwe, wychodzisz z założenia i dochodzisz do tezy. Jesli dla każdego x₁,x₂∊D i x₁<x₂ zachodzi: f(x₁)<f(x₂) to funkcja jest rosnąca.