zad Matma: Eta spoojrzysz?podstawe graniastoslupu jest rownoleglobok o obw 18 cm przekatne graniastoslupa maja dl.9,pierwiastek z 33 a krawedz podstawy bocznej ma dl.4 cm oblicz V

Eta: Witam ( już jestem , rysuję .... chwile potrwa...

Eta: zapytam , masz odp? ( bo dużo liczenia i nie wiem czy się nie pomyliłam?) wyszło mi : V = 64 cm³

Matma: nie mam:(

Eta: ok zaraz podam rozwiązanie ( cierpliwości

Matma: liczylasmoze bok rownolegloboku wyszlo mi pierwiastek z 69/4

Matma: a nei sory nie to zadanie

Matma: i jak tam?

Matma: az tak trudne?

Matma: umie ktos to zrobic

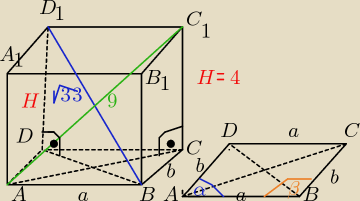Eta: V = P_p*H => V= P_p*4 P_p = a*b *sinα z trójkąta prostokatnegoACC₁ z tw Pitagorasa: IACI² = 81 −16 => IACI = √65 i z ΔBDD₁ ; IBDI² = 33 − 16 => IBDI = √17 z treści zad: 2a +2b = 18 => a =b = 9 => a = 9 −b , więc b€( 0,9) rozpatrujemy podstawę ( równoległobok: ze wzoru kosinusów mamy: a² +b² −2ab*cosα= IBDI² i a² +b² − 2ab*cosβ= IACI² ponieważ β=180^o −α więc cosβ= cos(180^o −α) = − cosα więc a² +b² −2ab*cosα= 17 a² +b² + 2ab*cosα= 65 dodając stronami otrzymamy: 2a² + 2b² = 82 /:2 to a² +b² = 41 i a +b = 9 rozwiazując układ tych równań otrzymasz: a = 5 cm b = 4 cm zatem należy wyznaczyć jeszcze miarę kąta α też ze wzorukosinusów:

	a2 +b2 − IIBDI2		3
cosα=		=
	2ab		5

więc sinα= √1 − cos²α= √1 − ⁹₂₅= p{¹⁶₂₅ = ⁴₅ więc P_P = a*b*sinα podstaw i wyznacz P−P i V

Eta: Co jesteś taka niecierpliwa? Pisałam ,że dużo liczenia

Eta: sorry , poprawiam chochliki: sinα= √¹⁶₂₅= ⁴₅ i oczywiście wyznacz P_p i V To juz proste i z pewnością sobie poradzisz Powodzenia.

Matma: o wow faktycznie dizkeuje Eta :

Eta:

Matma: Eta nei wiesz gdzie mickej?