Parzystość bra: Zbadać parzystość funkcji:

	x+2
f(x)=5
	x−1

	x+2
Nie potrafię dobrze napisać potęgi. Jest 5 do potęgi		.
	x−1

Bardzo proszę o pomoc. Pozdrawiam.

Bogdan: Najpierw wyznacz dziedzinę funkcji

bra: R\{1} ?

Bogdan: No to nie ma co sprawdzać, funkcja nie jest parzysta i nie jest nieparzysta (dziedzina w przypadku parzystości lub nieparzystości musi być symetryczna względem zera, np. gdyby dziedzina D = R \ {−1, 1} to można sprawdzać parzystość lub nieparzystość)

bra: Dziękuję a czy mogłabym jeszcze poprosić o pomoc w wyznaczeniu funkcji odwrotnej do tej funkcji? Gdy funkcja nie ma w sobie potęgi potrafię to zrobić, jednak za taką nie wiem jak się zabrać, nie wiem jak sprawdzić różnowartościowość, czy wystarczy porównać potęgi jeśli założymy, że f(x₁)=f(x₂) ?

Bogdan: Zalóżmy dla x≠1 i x₁ ≠ x₂ ⇒ x₂ − x₁ ≠ 0: 5^{(x₁+2)/(x₁−1)} ≠ 5^{(x₂+2)/(x₂−1)}

x1 + 2		x2 + 2
	≠		⇒ (x1 + 2)(x2 − 1) ≠ (x2 + 2)(x1 − 1)
x1 − 1		x2 − 1

x₁x₂ − x₁ + 2x₂ − 2 ≠ x₁x₂ − x₂ + 2x₁ − 2 ⇒ x₂ − x₁ + 2x₂ − 2x₁ ≠ 0 (x₂ − x₁) + 2(x₂ − x₁) ≠ 0 ⇒ 3(x₂ − x₁) ≠ 0 brak sprzeczności, więc funkcja przy dla x ≠ 1 jest równowartościowa. Korzystamy z: b = a^k ⇒ k = log_a b

	x + 2
y = 5(x+2)/(x−1) ⇒		= log5y wyznacz stąd x
	x − 1

bra: Dziękuję bardzo

Bogdan: nieładny zapis "przy dla", ma być "przy" albo "dla"

Bogdan: Dokończę. x + 2 = xlog₅y − log₅y ⇒ xlog₅y − x = log₅ + 2 ⇒ x(log₅y − 1) = log₅ + 2

	log5y + 2
x =
	log5y − 1

	log5 x + 2
Zamieniamy miejscami oznaczenia x i y: y =
	log5 x − 1

	log5 x + 2
Funkcja odwrotna f−1(x) =
	log5 x − 1

Proszę sprawdzić moje przekształcenia (wszędzie jest log₅y lub log₅x)

bra: Dziekuję tak się nad tym zastanawiałam, jak tu przekształcić tą potegę, a teraz już wszystko wiem bardzo przydatne informacje

bra: A jeśli chodzi o takie zadanie : |x³−1|<x²+x+1 Sprawdzam sobie dwa przypadki dla x∊(−∞,1) i dla <1,+∞) ?

bra: Przepraszam że tak męczę

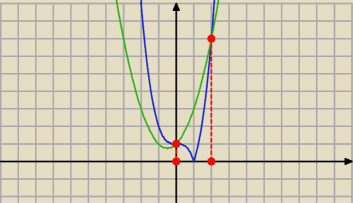
Bogdan: Dla x < 1: −x³ + 1 < x² + x + 1 ⇒ x³ + x² + x > 0 ⇒ x(x² + x + 1) > 0 ⇒ x > 0 x∊(0, 1) Dla x ≥ 1: x³ − 1 < x² + x + 1 ⇒ x³ − x² − x − 2 < 0 ⇒ (x − 2)(x² + x + 1) < 0 ⇒ x < 2 x∊<1, 2) Odp.: x∊(0, 2) Niebieski wykres: y = |x³−1|, zielony: y = x² + x + 1

bra: Dziękuje jeszcze raz

pigor: ..., np. tak : |x³−1| < x²+x+1 ⇔ |(x−1)(x²+x+1)| < x²+x+1 ⇔ |x−1| (x²+x+1 − (x²+x+1) < 0 ⇔ ⇔ (x²+x+1) |x−1| < 0 / : x²+x+1 >0 ⇔ |x−1| <0 ⇔ x∊∅ − nierówność sprzeczna .

pigor: ...ups, czyżbym ja sknocił , gdzie , poczekam, może przed snem dowiem się . ...

ICSP: pigor po drugim ⇔ włączyłeś przeniesione x² +x + 1 do nawiasu tak jakby stało przy nim |x−1| |x³ −1| < x² + x + 1 ⇔ |x−1| * (x² + x + 1) < x² + x + 1 ponieważ x² + x + 1 dla każdego x jest > 0 mogę podzielić nierówność przez x² + x + 1. zatem : |x−1| < 1 ⇒ x ∊ (0;2)

pigor: ..., tak jest , u mnie błąd pod koniec powinno być |x−1|−1 < 0 ⇔ |x−1| < 1 ⇔ −1< x−1< 1 ⇔ 0 < x < 2 −−−−− a więc dobranoc . ...

pigor: ..., dzięki ICSP , , teraz spokojnie mogę iść spać . ...

pigor: ..., fajny przykład, dlatego jeszcze raz : |x³−1| < x²+x+1 ⇔ |(x−1) (x²+x+1)| < x²+x+1 ⇔ |x−1| (x²+x+1) − (x²+x+1) < 0 ⇔ ⇔ (x²+x+1) (|x−1|−1) < 0 / : x2+x+1 >0 ∀x∊R ⇔ |x−1| −1 < 0 ⇔ |x−1| < 1 ⇔ ⇔ −1 < x−1 < 1 /+1 ⇔ 0 < x < 2 ⇔ x∊(0,2) . ...