Zapisz wzór funkcji f w postaci kanonicznej bartek: Dana jest funkcja kwadratowa określona wzorem: f(x) = 2x² − 5x −3. a) Zapisz wzór funkcji f w postaci kanonicznej b) sporządź wykres danej funkcji f. c) określ maksymany przedział, w którym funkcja f jest malejąca d)oblicz współrzędne punktów przecięcia wykresu funkcji f oraz funkcji g opisanej wzorem gg(x) = −5x −1.

Beti: a) oblicz p i q, a następnie podstaw je do wzoru: y = a(x−p)²+q

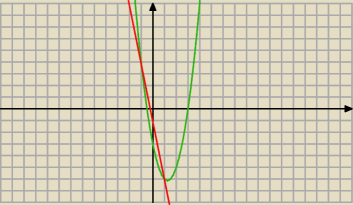
bezendu: jedna kratka to 1 jednostka policz p i q czerwona kreska to −5x−1 zielony wykres to Twoja funkcja 2x²−5x−3

bartek: i to już całe zadanie zrobione?

bezendu: nie

pigor: ..., np. tak a) f(x)= 2x²−5x−3= 2(x²−⁵₂x−³₂)= 2(x²−2*⁵₄x+²⁵₁₆−²⁵₁₆−²⁴₁₆= = 2(x−⁵₄)²− ²⁵⁺²⁴₈= 2(x−⁵₄)²− 6¹₈ − postać kanoniczna , −−−−−−−−−−−−−−−−−−−−−−−−−− c) x∊(−∞ ; ⁵₄> − maksymalny przedział w którym f jest malejąca , −−−−−−−−−−−−−−−−−−−−− d) f(x)= g(x) ⇔ 2x²−5x−3= −5x−1 ⇔ 2x²= 2 ⇔ x²=1 ⇔ |x|=1 ⇔ ⇔ x=−1 lub x=1 ⇔ x∊{−1,1} . ...