Trapez równoramienny Żabka: Oblicz długość podstaw trapezu równoramiennego o polu 8√2, w którym przekątna jest trzy razy dłuższa od wysokości, a ramię ma długość 4.

Janek191: Mamy trapez ABCD. a = I AB I, b = I CD I, c = I AD I = I BC I = 4 oraz h = I CE I I AC I = 3 h P = 8√2 −−−−−−−−−−−−−−−−−− Niech I AE I = x i I EB I = y i x + y = a Z tw. Pitagorasa mamy x² + h² = ( 3 h)² y² + h² = c² = 16 ⇒ y² = c² − h² oraz P = x*h = 8√2 zatem x² = 9 h² − h² = 8 h² ⇒ x = 2 √2 h czyli 2 √2 h* h = 8 √2 / : 2 √2 h² = 4 h = 2 ===== x*2 = 8 √2 ⇒ x = 4 √2 y² = c² − h² = 16 − 4 = 12 = 4*3 ⇒ y = 2 √3 a = I AB I = x + y = 4 √2 + 2 √3 b = x − y = 4 √2 − 2 √3 Odp. a = 2*( 2 √2 + √3), b = 2*( 2 √2 − √3) ========================================

Eta:

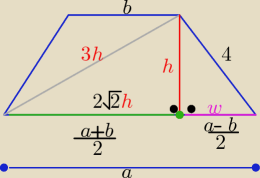
a+b
	= 2√2h to P= 2√2h*h= 8√2 ⇒ h2=4 ⇒ h=2
2

to a+b= 2√2h= 8√2 i w²= 4²−h² ⇒ w²=12 ⇒ w=2√3 to a−b= 4√3 + −−−−−−−−−−−−− 2a= 8√2+4√3 ⇒ a= 2(2√2+√3) b= 8√2−4√2−2√3 ⇒ b= 2(2√2−√3)