Geometria płaska - pole trójkąta liceum... podstawą trójkąta równoramiennego ABC
xyz:
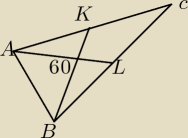
Podstawą trójkąta równoramiennego ABC jest bok AB. Środkowe AL i BK przecinają się w punkcie S
pod kątem 60° (patrz rysunek). Wiadomo, że pole trójkąta ABS jest równe \sqrt{3}.
a)Oblicz długość boków trójkąta ABC.
b) Czy kąt ACB jest równy 30°? odpowiedź uzasadnij.
6 cze 18:49
pigor: ..., np. niech dla uproszczenia zapisu długości AC=BC=2a , AB=c i S dzieli środkowe
na AS=BS=2k to KS=LS=k − z własności tych środkowych Δ równoramiennego ,
a wtedy katy SAb=SBA =60
o , a więc ΔABS − równoboczny o boku 2k , czyli
AB=AS=BS=2k , więc z warunków zadania
a) P
ΔABS=
√3 ⇔
14*(2k)
2√3=
√3 ⇔ k
2=1 ⇒
k=1 czyli
AB=2 ,
zaś np. z ΔASK i tw. cosinusów
a
2=1
2+2
2−2*2*1cos120
o ⇔ a
2= 5−4cos(90
o+30
o) ⇔ a
2= 5+4sin30
o ⇔
⇔ a
2=5+2 ⇒
a=√7, zatem
AC=BC= 2√7
−−−−−−−−−−−−−−−−−−−−−−−−
b) może teraz spróbujesz sam(a)
, albo ktoś inny pomoże . ...
6 cze 19:36
pigor: .... być może gdzieś się walnąłem, albo ... gorzej,
bo tak na szybko, coś mi nie gra z tym b) ...
6 cze 19:41
xyz: wielkie, dzięki, wszystko zrobiłeś dobrze. Postaram się zrobić podpunkt b). Jak mi się uda to
wrzucę może się komuś przyda
6 cze 20:04
pigor: ... a to ja spanikowałem bo z tw, cosinusów dla ΔABC
wyszło mi, że cosACB >1, ale teraz jeszcze raz zrobiłem
i wyszło mi tak :
b) 2
2=4*7+4*7−2*2
√7*2
√7cos(ACB) ⇔ 4=56−56coACB ⇔
| | 52 | | 13 | |
⇔ cos(ACB)= |
| ⇔ cosACB= |
| ⇒ ACB ≈ 22o ≠ 30o . .. |
| | 56 | | 14 | |
6 cze 20:17
nieuk:
17 gru 16:15