Funkcja bra: Jak wygląda funkcja odwrotna do funkcji:

	x2+1
f(x)=		?
	x2−1

Czy mógłby mi ktoś pomóc? nie wiem co powinnam zrobić.

ICSP: f(2) = f(−2) − wyciagnij wnioski

bra: Nie istnieje funkcja odwrotna? bo funkcja nie jest różnowartościowa?

ICSP:

bra: A gdyby jednak była, to co powinnam zrobić po kolei? Bardzo proszę o pomoc

asdf: mozesz skrocic dziedzine i narysowac dla jakiegos przedzialu. Tak samo nie znajdziesz funkcji odwrotnej dla sinusa, cosinusa, x² itd..trzeba zrobic z niej roznowartosciowe funkcje − tzn. wlasnie zmniejszyc przedział argumentow dla ktorych funkcja jest roznowartosciowa.

Janek191: Np. y = x² − 1; x ≥ 0 Wyliczam z tego x x² = y + 1 x = √ y + 1 ; dla y ≥ − 1 Zamieniam zmienne y = √ x + 1 − funkcja odwrotna do funkcji y = x² − 1

ICSP: jest to funkcja parzysta wiec zachodzi f(x) = f(−x) obetnę dziedzinę do x > 0 , x ≠ 1

	x2+1
y =
	x2−1

	y2 + 1
x =
	y2−1

	y2−1 + 2
x =
	y2−1

	2
x = 1 +
	y2−1

x−1		1
	=
2		y2−1

	x−1
y2 =		+ 1
	2

	x−1
y = √		+ 1
	2

i niech lepiej ktoś to sprawdzi

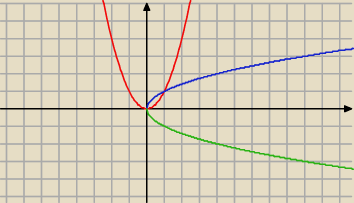
asdf: tu prosty przykład: y = x² można otrzymać: y² = x y = √x (dla x > 0) lub y = −√x (argumenty ujemne). Teraz zalezy juz od Ciebie, ktory wykres jest Ci bardziej potrzebny (np. przy liczeniu pól ograniczonych krzywymi..)

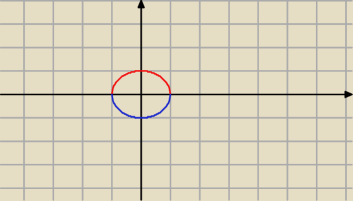
asdf: a tu kolejny przykład (tylko to nie jest funkcja, ale mozesz to rozbić): y²+x² = 1 y² = 1−x² y = √1−x² lub y = −√1−x²

bra: Dziękuję bardzo, teraz już wiem jak postępować w kolejnych przykładach Te informacje bardzo mi się przydały