| 2x2 | ||
f(x)= | ||
| x+1 |
| x2+3 | ||
f(x)= | ||
| x−1 |
| x2 | ||
F(x)= | ||
| 1+x2 |
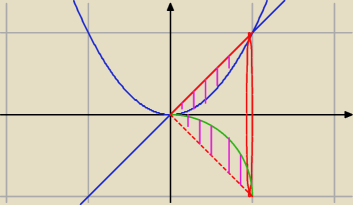No dobra spróbuję to wytłumaczyć, bo mam nadzieję, że chcecie zrozumieć a nie tylko przepisać.
zad 1.
a) Najpierw trzeba zerknąć do wzorów i zobaczyć jaki wzór określa objętość bryły powstałej
poprzez obrót dookoła OX :
π ∫ab f2(x) dx
Wyznaczmy najpierw miejsce przecięcia się tych dwóch krzywych, określi nam to granice
całkowania :
x2 = x
x2 − x = 0
x(x − 1) = 0
x = 0 v x = 1
Ok to będą nasz a i b we wzorze z góry.
Na rysunku narysowałem te dwie krzywe. Fragment, który zakreskowałem jest po obrocie wokół osi
OX szukaną naszą objętością. Jak policzyć to "coś". Najłatwiej będzie poprzez różnicę
objętości dwóch innych brył. Widzimy na obrazku, że prosta y = x w przedziale x ∊<0, 1> po
obrocie staje się stożkiem (narysowany na czerwono). Z drugiej strony parabola y = x2 w tym
samym przedziale po obrocie staje się "niepełnym" (zjedzonym z dwóch stron) stożkiem (zjedzony
stożek to jest ten po obrocie y = x). Teraz zauważmy, po odjęciu objętości "niepełnego" stożka
(y = x2) od objętości "pełnego "stożka" otrzymamy naszą szukaną objętość!
Przystąpmy więc do liczenia. Szukaną objętością V będzie więc :
| 1 | 1 | |||
V = π ∫10 x2 dx − π ∫10 x4 dx = π [ | x3]10 − π [ | x5]10 = | ||
| 3 | 5 |
| 1 | 1 | π | π | 2π | ||||||
= π( | − 0) − π( | − 0) = | − | = | ||||||
| 3 | 5 | 3 | 5 | 15 |
