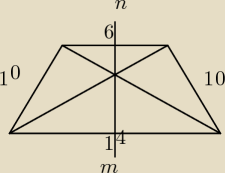
ratunku lipa: Ratunku bo to już noc naprawdę nikt nie umie tego zadania. Podstawy trapezu mają 6 i 14 cm. Przez punkt przecięcia przekątnych poprowadzono prostą, która przecina ramiona w punktach M i N Onliczyć MN

b.: Jest tu trochę za mało danych do tego −− np. czy ta prosta jest równoległa do podstaw?

Matma:

lipa: Ta prosta przecina ramiona ale już chyba znalazłam rozwiązanie trzy podejścia i jest sukces

zero: Jeśli jest równoległa do podstaw to jej dlugość jest

	2
8
	3

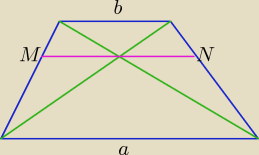
Bogdan: Punkty M, N leżą na ramionach trapezu, a nie na podstawach. Brak w zadaniu informacji, czy jest to trapez równoramienny, nieuzasadnione jest więc przyjęcie, że ramiona mają długość 10. Jeśli odcinek MN jest równoległy do podstaw, to jego długość jest równa średniej

	2ab		2 * 14 * 6
harmonicznej długości podstaw, czyli |MN| =		=
	a + b		14 + 6

lipa: Bogdan jesteś niezły