w trójkącie ABC Karolina9555: .W trójkącie ABC |AC|=a,|BC|=b(a>b)i|CD|=d, gdzie CD jest odcinkiem leżącym na dwusiecznej kąta ACB, zawartym w trójkącie. Oblicz długośc boku AB tego trójkąta. (Wskazówka: Oznacz |AD|=x, |DB|=y. Zastosuj twierdzenie o podziale boku trójkąta przez dwusieczną kąta wewnętrznego, a następnie oblicz x i y, korzystając z twierdzenia cosinusów dla trójkątów ACD i DBC.)

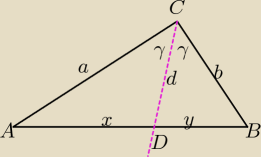
Mila: Z tw. o dwusiecznej kata:

a		b		ay
	=		⇔x=
x		y		b

	ay		a		a+b
x+y=|AB|⇔|AB|=		+y⇔|AB|=y(		+1)=y*		⇔
	b		b		b

	a+b
AB=y*
	b

Z tw. cosinusów: x²=a²+d²−2ad cosγ y²=b²+d²−2bd cosγ

	1
PΔABC=		a*b*sin(2γ)
	2

	1		1
PΔABC=		ad *sinγ+		db*sinγ⇔
	2		2

1		1		1
	a*b*sin(2γ)=		ad *sinγ+		db*sinγ⇔
2		2		2

a*b*2 sinγ*cosγ=ad *sinγ+db*sinγ /:sinγ 2ab*cosγ=ad+bd

	ad+bd
cosγ=
	2ab

	ad+bd
y2=b2+d2−2bd*
	2ab

	d*(ad+bd)		ab2+ad2−ad2−bd2
y2=b2+d2−		⇔y2=
	a		a

	ab2−bd2
y2=
	a

	√ab2−bd2
y=
	√a

	a+b		√ab2−bd2
|AB|=		*
	b		√a