Całka podwójna - obszar D lejdi-: ∫∫ (3xy−5x)dxdy D: y=x², y=4, x≥0 prosze o pomoc w napisaniu obszaru

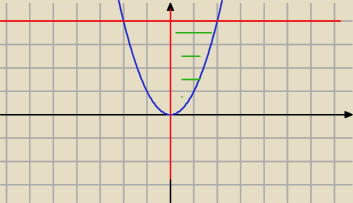
Basia: y ∊<0;4> x∊<0, √y>

Vizer: Wyznaczamy punkty przecięcia się z naszymi krzywymi wyznaczającymi obszar, na którym będziemy całkować : x² = 4 x = 2 v x = −2 I zapisujemy całkę : ∫²₋₂ dx ∫⁴_x² (3xy − 5x) dy = ... Albo łatwiejszą w rachunkach : 2 * ∫²₀ dx ∫⁴_x² (3xy − 5x) dy = ...

Basia: x≥ 0 ma być przeoczyłeś

Vizer: Witaj Basiu A faktycznie nie doczytałem To druga całka wchodzi w grę tylko bez mnożenia razy 2. Dzięki za czujność Basia!

lejdi-: ∫₀² dx ∫⁴_x2 (3xy − 5x) dy =

lejdi-: czyli tak jest poprawnie ?

Vizer: Tak jest poprawnie.

Vizer: I tak jak Basia zrobiła też jest poprawnie tylko zmieniła kolejność całkowania.

lejdi-: Super dziękuję bardzo a mam jeszcze problem z taką całką ∫∫ ( e^x2 + y²) dx dy D: x²+y²≤4 x² +y²≥1

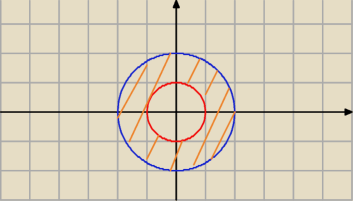
Vizer: Taki mamy obszar całkowania jak na rysunku. Ciężko będzie policzyć całkę z tak określonych krzywych, dlatego zamieniamy współrzędne na biegunowe : 0 ≤ φ ≤ 2π (kąt zakreśla nam ten obszar w 360 st) 1 ≤ r ≤ 2 (różnica promieni) |J| = r (jakobian konieczny przy zmianie na biegunowe) Nasza całka ma więc postać : ∫^2π₀ dφ ∫²₁ (e^r2cos2φ + r²sin²φ)r dr = ...

lejdi-: a taka całka tzn chodzi o obszar D ∫∫(2xy)dxdy D: y=2−x², y=−2 x>0