Równania prostej Ona_18: Wierzchołki trójkąta mają współrzędne: A=(−1,−2) B=(5,−1) C=(2,5) Znajdź równanie prostej przechodzącej przez : a) punkt A i równoległej do boku BC b) środek odcinka AB i równoległej do boku AC c) środek odcinka BC i prostopadłej do boku AC

AROB: Pomagam

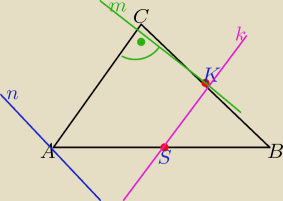
AROB: a) prosta n:

	yC−yB		5+1
aBC =		=		=−2
	xC−xB		2−5

n∥ BC ⇒ a_n = a_BC =−2 równanie prostej n: y − y_A = a_n ( − x_A) y + 2 = −2(x+1) ⇒ y = −2x − 4

	xA+xB		−1+5
b) prosta k : S(xS,yS), xS =		=		= 2
	2		2

	yA+yB		−2−1		3		1
yS =		=		= −		= −1
	2		2		2		2

	1
Czyli S(2,−1		)
	2

	yC−yA		5+2		7
aAC=		=		=
	xC−xA		2+1		3

	7
k∥AC ⇒ ak = aAC =
	3

równanie prostej k: y − y_S = a_K(x−x_S)

	1		7		7		37
y + 1		=		(x−2) ⇒[C[y =		x −
	2		3		3		6

c) prosta m:

	7		1		3
aAC =		, m⊥AC ⇒ am = −		= −
	3		aAC		7

	xB+xC		5+2		1
K(xK,yK), xK =		=		=3
	2		2		2

	yB+yC		−1+5
yK =		=		= 2
	2		2

	1
Czyli: K(3		,2)
	2

równanie prostej m: y − y_K = a_m(x−x_K)

	3		7		3		1
y − 2 = −		(x −		) ⇒ y=−		x + 3
	7		2		7		2