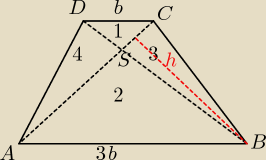
 PABCD=120
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa .
PABCD=120
Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa .
| 1 | ||
ΔDCS∼ΔABS (ceha kkk) w skali k= | ||
| 3 |
| 1 | 1 | |||
P3= | P2 ( ΔCSB iΔBSA maja tę samą wysokość, SC= | SA) | ||
| 3 | 3 |
| 30 | 15 | |||
x= | = | |||
| 4 | 2 |
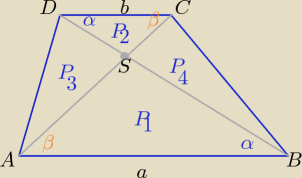 trójkąty ABS i CDS są podobne w skali k= 3
P1=k2*P2 , P3=P4= k*P2 to:
P(tr)= k2P2+2k*P2+P2 = (k2+2k+1)*P2 = (k+1)2*P2
P(tr)= (k+1)2*P2 ⇒ 120=16*P2 ⇒ P2= 7,5 cm2
P1= k2*P2= 9*7,5= 67,5 cm2
P3=P4= k*P2= 3*7,5= 22,5 cm2
trójkąty ABS i CDS są podobne w skali k= 3
P1=k2*P2 , P3=P4= k*P2 to:
P(tr)= k2P2+2k*P2+P2 = (k2+2k+1)*P2 = (k+1)2*P2
P(tr)= (k+1)2*P2 ⇒ 120=16*P2 ⇒ P2= 7,5 cm2
P1= k2*P2= 9*7,5= 67,5 cm2
P3=P4= k*P2= 3*7,5= 22,5 cm2