Dwusieczne
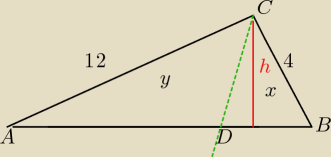
dubikz: W trójkącie ABC poprowadzono dwusieczną z punktu C, która przecięła bok AB w punkcie D, wiedząc
że AC = 12 cm, BC = 4 cm, a pole trójkąta ABC jest o 6√3 większe od pola trójkąta DBC. Oblicz
pole trójkąta ABC.
Prosiłbym o rozwiązanie zadania z wytłumaczeniem, jest mi pilnie potrzebne na jutrzejszy dzień.
Z góry dziękuję !
4 cze 22:43
Mila:
To dlaczego tak późno zabrałeś się za pracę?
Może coś wymyślę.
PΔABC=x+6√3
P
ΔADC=y
P
ΔBDC=x
| y | | AD | |
| = |
| −Δ mają tę samą wysokość |
| x | | DB | |
Z tw o dwusiecznej kąta mamy:
| y | | AD | | y | | 3DB | |
| = |
| ⇔ |
| = |
| =3 |
| x | | DB | | x | | DB | |
y=3x
x+3x=P
ΔABC⇔4x=x+6
√3
3x=6
√3
x=2
√3
P
ΔABC=6
√3+2
√3=8
√3
5 cze 00:07
 To dlaczego tak późno zabrałeś się za pracę?
Może coś wymyślę.
PΔABC=x+6√3
PΔADC=y
PΔBDC=x
To dlaczego tak późno zabrałeś się za pracę?
Może coś wymyślę.
PΔABC=x+6√3
PΔADC=y
PΔBDC=x