Błagam, pomóżcie... maja: znaleźć współczynnik kierunkowy prostej przechodzącej przez punkt A=(1,27) i odcinającej w I ćwiartce układu współrzędnych najkrótszy odcinek. jaka jest długość tego odcinka?

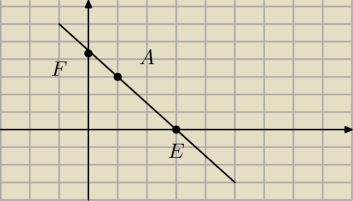
Nienor: U mnie A=(1,3), bo łatwiej narysować, ale w twoim chodzi o to samo

	−b
F=(0,b) E=(		, 0) a≠0
	a

Od razu widzać, że a=0 odpada, bo wtedy taki odcinek ma długość nieskończoną.

	b2		b
|FE|=√b2+		=		√a2+1 (*) z tw. Pitagorana
	a2		a

Wykorzystajmy teraz danu punkt A=(1,3) 3=a+b ⇒ b=3−a Podstawiamy to do wzoru (*):

	3−a
|FE|=		√a2+1
	a

Liczysz pochodną, rozważasz minima i gotowe, musisz tylko pamiętać, że a<0, bo funkcja musi być malejąca.

PW: Prosta ma równanie y=ax+b (jeśli nie jest pionowa). Dla x=1 i y=27 obliczamy 27=a•1+b b=27−a, a więc prosta ma równanie (1) y=ax+(27−a) Żeby prosta coś odcinała w pierwszej ćwiartce, musi być a<0 (tu warto naszkicować rysunek, nawet bez zachowania proporcji − autor złośliwie dał 27 "żeby się nie zmieściło"). Wiadmo, że prosta przecina osie w punktach (0,y₀) i (x₀,0). Po podstawieniu do (1) y₀=a•0+(27−a) i 0=a•x₀+(27−a) y₀=27−a, a•(x₀−1)=−27

	27
x0=1−
	a

Mamy zatem punkty przecięcia prostej z osiami:

	27
A=(0, 27−a) i B=(1−		, 0)
	a

Obliczyć odległość od A do B − otrzymamy funkcję zmiennej a∊(−∞,0), którą trzeba zbadać − dla jakiej a osiąga minimum (to będzie szukany współczynnik kierunkowy), po czym to minimum policzyć.