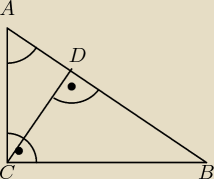
 Trójkąt ABC jest prostokątny. Punkt D jest spodkiem wysokości opuszczonej na przeciwprostokątną
AB oraz 3|AD|=|DB|. Wykaż, że |∡CAD|=60 stopni (czyli mam udowodnić że kąt CAD ma 60 stopni)
Trójkąt ABC jest prostokątny. Punkt D jest spodkiem wysokości opuszczonej na przeciwprostokątną
AB oraz 3|AD|=|DB|. Wykaż, że |∡CAD|=60 stopni (czyli mam udowodnić że kąt CAD ma 60 stopni)
| AD | h | x | h | |||||
⇔ | = | ⇔ | = | |||||
| h | DB | h | 3x |
| h | ||
tgA= | ||
| |AD| |
| x√3 | ||
tgA= | ⇔ | |
| x |
| h | 3x | ||
= | |||
| x | h |
| h | x√3 | |||
tgα= | = | =√3 | ||
| x | x |

