funkcja Karolina: Dana jest funkcja f(x) = |x−1| − | x+2| dla x∊R a) wyznacz zbiór wartości funkcji f dla x∊(−∞,−2) b) naszkicuj wykres tej funkcji c) podaj jej miejsca zerowe d) wyznacz wszystkie wartosci parametru m dla ktorych f(x)=m nie ma rozwiązania

Bogdan: f(x) = |x − 1| − |x + 2| Dla A: x∊(−∞, −2) f(x) = −(x − 1) + (x + 2) ⇒ f(x) = 3, funkcja stała. Dla B: x∊<−2, 1) f(x) = −(x − 1) − (x + 2) ⇒ f(x) = −2x − 1. Dla C: x∊<1, +∞) f(x) = (x − 1) − (x + 2) ⇒ f(x) = −3, funkcja stała.

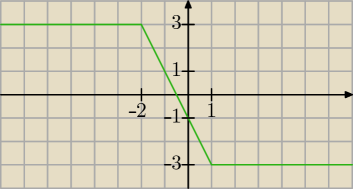
Bogdan: a) Zbiór wartości dla x∊(−∞, −2): ZW_f: y∊{3}. c) Miejsce zerowe należy do przedziału <−2, 1), w którym funkcja f(x) wyraża się wzorem: f(x) = −2x − 1 f(x) = 0 ⇔ −2x − 1 = 0 ⇒ x = .... d) Równanie f(x) = m: − nie ma rozwiązań dla m∊(−∞, −3)∪(3, +∞), − ma 1 rozwiązanie dla m∊(−3, 3), − ma nieskończenie wiele rozwiązań dla m∊{−3, 3}. Wyobrażamy sobie dwie linie: y = |x − 1| − |x + 2| (zielona linia) i y = m (wykres funkcji stałej). Wyznaczamy wspólne punkty tych linii.