Planimetria goo: W trapezie o podstawach długości a i b poprowadzono odcinek równoległy do podstaw i dzielący pole trapezu na polowy. Wyznacz długość tego odcinka. Proszę o rozwiązanie, nie wiem co zrobić.

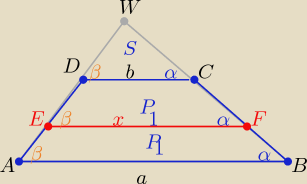
Eta: Trójkąty EFβW i DCW są podobne i trójkąty ABW i DCW z cechy (kkk)

	x		a
skala podobieństwa (*) k1=		i (**) k2=
	b		b

	P1+S		x		2P1+S		a
to (*)		= k2= (		)2 i (**)		= (		)2
	S		b		S		b

	P1		x2		P1		P1		a2
(*)		+1=		i (**)		+		+1=
	S		b2		S		S		b2

	P1		x2		x2		P1		a2
zatem:		=		−1 ⇒ (**)		+		=
	S		b2		b2		S		b2

	x2		x2		a2
(**)		+		−1=		/ *b2
	b2		b2		b2

x²+x² −b²= a² 2x²= a²+b² /:2

	a2+b2
x2=
	2

	a2+b2
x= √		−−−− ten odcinek ma długość równą średniej kwadratowej
	2

długości podstaw trapezu

pigor: ..., lub niech h,H − długości wysokości trapezów ABFE i EFCD odpowiednio, G∊EF i H∊AB takie, że GC||HF||AD i |GF|=x−b, |HB|=a−x, gdzie b< x< a i |EF|=x=?, to z warunków zadania

	x−b		H
12(a+x)h= 12(b+x)H i		=		, bo ΔCGF∼ ΔFHB (cecha kkk) ⇔
	a−x		h

a+x

H

x−b

H

a+x

x−b

⇔

=

i

=

⇔

=

⇔

b+x

h

a−x

h

b+x

a−x

⇔ x²−a²= b²−x² ⇔ 2x²= a²+b² ⇒ x=¹₂√a²+b² . ...

pigor: ..., oj coś źle na końcu policzyłem, a więc jeszcze raz 2x²=a²+b² ⇔

	√a2+b2
⇔ x2= 12(a2+b2) ⇒ x=		⇔ x= √12(a2+b2). ...
	√2

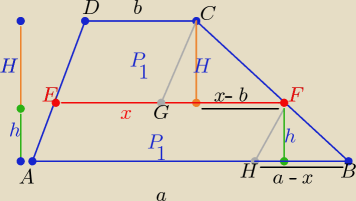Eta: Dorysuję rysunek, do rozwiązania podanego przez pigora ( bo nie chce Mu się rysować

pigor: oj, tak , nie chce, no i to byłoby już za wiele ...

Wojtek: To najtrudniejsze zadanie w całym pęcie Kiełbasy.