Całka fiesław: Obliczyć całkę ∫∫ (2x+y) dxdy , gdzie obszarem całkowania jest obszar ograniczony liniami x=0, y=0, x+y=3 Bardzo proszę o jakąkolwiek pomoc w rozwiązaniu zadania

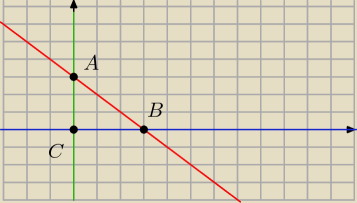
Nienor: Obszar po którym całkujesz to wnętrze trójkąta. A=(0,3) B=(3,0) C=(0,0) x∊[0,3] y∊[0,−x+3]

	1
∫∫(2x+y)dxdy=∫30 dx∫3−x0 (2x+y)dy=∫30[2xy+		y2]3−x0dx=
	2

	1
∫30(2x(3−x)+		(3−x)2)dx=... powinieneś dać radę.
	2

Vizer:

	1
∫30 dx ∫3−x0 (2x + y) dy = ∫30 [2xy +		y2]3−x0 dx =
	2

	1
= ∫30 (2x(3 − x) +		(9 − 6x + x2)) dx =
	2

	9		1
= ∫30 (6x − 2x2 +		− 3x +		x2)dx =
	2		2

	3		9		1		3		9
= ∫30 (−		x2 + 3x +		) dx = [ −		x3 +		x2 +		x ]30 =
	2		2		2		2		2

	27		27		27		27
= −		+		+		=
	2		2		2		2

fiesław: wielkie dzięki. wyszło mi 27/2, dobrze ? mam jeszcze problem z jednym zadaniem w którym należy obliczyć objętość bryły. pomożesz ?

Nienor: Jak bedę wiedziała A jak nie to myślę, że Vizer się skusi

fiesław: Polecenie brzmi: Obliczyć obj. bryły ograniczonej powierzchniami x² + y² =1 , x+y+z=3, z=0. Proszę o pomoc

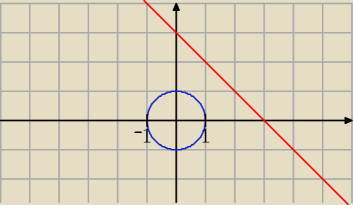
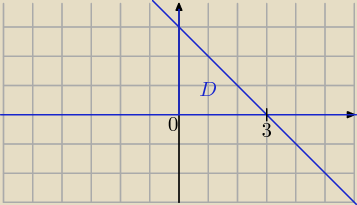
Vizer: x² + y² = 1 to w układzie OXYZ jest to walec, który w płaszczyźnie OXY jest okręgiem o środku (0,0) i promieniu r = 1. z = 3 − x − y to płaszczyzna w OXYZ, i prosta y = 3 − x w OXY (na czerwono) Jak widać płasczyzna nie zaburza nam obszaru, wktórym będziemy całkować, więc naszym obszarem będzie okrąg. Jak więc mamy do czynienia z okręgiem to automatycznie powinniśmy zdać sobie sprawę z tego, że bez przejścia na współrzędne walcowe będzie ciężko. Nasze granice całkowania będą więc następujące : 0 ≤ φ ≤ 2π (kąt zaznacza, obrysowuje nam cały okrąg) 0 ≤ r ≤ 1 (wynika z faktu, ze promień okręgu równy 1) 0 ≤ z ≤ 3 − x − y (ograniczenie naszej bryły przez te dwie płaszczyzny) J = r (jakobian jest konieczny przy zamienie na wsp. walcowe) Zapisujemy wreszcie naszą całkę będącą objętością wyznaczonej bryły : ∫₀^2π dφ ∫¹₀ dr ∫^3−x−y₀ r dz = ... Dokończ. Mam nadzieję, że wszystko dobrze. Może Nienor jeszcze zrobiła podczas mojego pisania

fiesław: dzięki wielkie. a jak mam rozumieć to, że obszar jest ograniczony powierzchnią z=0

Vizer: z = 0 to jak to nazywam wykładzina układu współrzędnych, czyli płaszczyzna obejmujaca w OXYZ cały obszar układu OXY.

fiesław: aha, czyli nie ma to nic wspólnego z tym ,że w równaniu płaszczyzny , za "z" mogę sobie podstawić zero, tak ? A jak zmieniła by się sytuacja gdybyśmy nie mieli podanej informacji o "z" ?

Vizer: No coś być musi tak samo jak mamy pojedynczą całkę, czyli obracamy sie w układzie OXY, to zawsze jakaś krzywa ten obszar nam domyka. Tutaj mogą to być jakieś płaszczyzny, walce, sfery, stożki itd.

fiesław: hmm. a jest taka możliwość żeby wkleić to do jakiegoś wolframa, żeby zobaczyć jak ta figura wgl wygląda ? bo jakoś nie mogę sobie jej wyobrazić w żaden sposób

fiesław: a czy jest możliwość zapisania tej objętości poprzez całkę podwójną, a nie potrójną ?

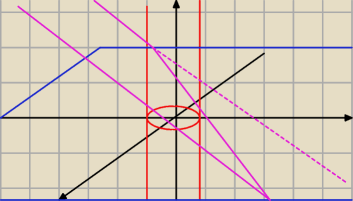
Vizer: Z tym to ciężka sprawa jest niestety Na czerwono walec, na niebiesko z = 0 na fioletowo (chyba taki kolor?) z = 3 − x − y. Może słabo widać, bo cięzko mi tutaj to narysować ale jak widać z = 0 przekraja nasz nieskończony walec na pół, płaszczyzna z = 3− x −y kroi nam go jakby "na ukos" od góry co nam daje bryłę walca odkrojonego kawałek na górze. Mam nadzieję, że dobrze wytłumaczyłem.

fiesław: rozumiem dzięki wielkie.

Vizer: Można podwójną ∫^2π₀ dφ ∫¹₀ r * (3 − rcosφ − rsinφ − 0) dr A i na górze z potrójną całką troche zkiepściłem, bo w trzeciej całce niezamieniłem x i y na współrzędne biegunowe więc ta całka powinna wyglądac tak : ∫^2π₀ dφ ∫¹₀ ∫^{3−rcosφ−rsinφ}₀ r dz

Vizer: A z tą cieżką sprawą to odnosiło się do namalowania w wolframie tych wszystkich powierzchni, bo na podwójną jak widać da się zamienić. Możliwe, że sa programy co by to narysowały, znam jeden geogebra, byc może on to narysuje, ale ja nie znam za dobrze tego programu.