proszę o pomoc bo mi niestety wychodzi inny wynik :(
Lila: Pole rombu ABCD jest równe 32. Wyznacz współrzędne punktów B i D, jeśli: A(2,3), C(4,1). Ma
wyjść B(−5,−6) i D(11,10)
4 cze 17:14
aniabb:
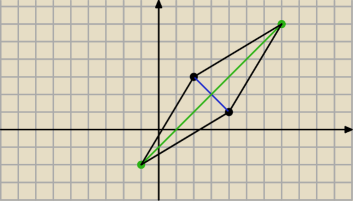
d1•d2/2=32
√2•d2=32
d2= 16
√2
więc 4
√2 w górę i w dół
B(−1;−2) D(7;6)
mi też wychodzi inny

4 cze 17:33
Lila: dziękuję

będę kombinować dalej ...
4 cze 17:38
Tomek: a mi wyszło dobrze:
długość odcinka |AC|=16
√2
zatem odcinek |SB|=|SD|=8
√2
S=środek odcinka |AC|
S=(3,2)
teraz wyznaczyłem równanie prostej AC:
x+y−5=0
teraz równanie prostej BD która jest prostopadła do prostej AC i przechodzi przez środek tego
odcinka (punkt S)
równanie:
y=x−1
a więc punkt B i D mają współrzędne : (x, x−1)− bo prosta BD przechodzi przez te punkty
ze wzoru na odległość punktu B od prostej x+y−5=0 które wynosi 8
√2 wyszła równość :
wynika z tego ze x=11 lub x=−5
y=10 lub y=−6
czyli B=( 11, 10) D=(−5, −6)

mam nadzieje ze wszystko jasne, moze da się krócej ale ja zawsze wolałem tak robić

4 cze 18:00
4 cze 20:37
aniabb: wiem gdzie miałam błąd..podzieliłam 16/2 i wyszło mi 4

a u Tomka to nie AC miało być 16
√2 a BD

tak jak u mnie

4 cze 20:42
aniabb:
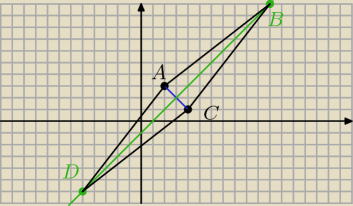
4 cze 20:44
 d1•d2/2=32
√2•d2=32
d2= 16√2
więc 4√2 w górę i w dół
B(−1;−2) D(7;6)
mi też wychodzi inny
d1•d2/2=32
√2•d2=32
d2= 16√2
więc 4√2 w górę i w dół
B(−1;−2) D(7;6)
mi też wychodzi inny 
 będę kombinować dalej ...
będę kombinować dalej ...
 mam nadzieje ze wszystko jasne, moze da się krócej ale ja zawsze wolałem tak robić
mam nadzieje ze wszystko jasne, moze da się krócej ale ja zawsze wolałem tak robić 




 a u Tomka to nie AC miało być 16√2 a BD
a u Tomka to nie AC miało być 16√2 a BD  tak jak u mnie
tak jak u mnie 
