Zadanie optymalizacyjne Borixon: Okno ma kształt prostokąta zakończonego na górze trójkątem równobocznym. Obwód wynosi 2m. Jaka powinna być długość podstawy prostokąta, aby przy obwodzie równym 2m powierzchnia okna była największa ?

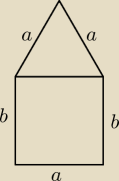
wredulus_pospolitus: obw = 3a + 2b = 2

	a2√3
pole = a*b +
	4

z pierwszego wyznacz 'b' i podstaw do równania na pole ... wyznacz ekstremum (maksimum ... wierzchołek paraboli) tego równania kwadratowego

Borixon:

	2(√3+6)
Podejrzewam że coś poszło nie tak skoro wynik jest równy		?
	33

wredulus_pospolitus: hmmm zobaczmy b = 1 − 1.5a

	a2√3
pole = a − 1.5a2 +
	4

jako że leń jestem ( i nie pamiętam wzoru na wierzchołek paraboli) to liczę z pochodnej:

	a√3
1 − 3a +		= 0
	2

−6a + a√3 = −2

	−2
a =
	√3−6

	2*(√3+6)
a =
	33

no i mi wyszło tyle samo

Borixon: no to dzięki