prosze o pomoc
??: jak rozwiązać ukłąd równań jeden z wyznaczeniem t a drugą z pdostawieniem y ? czyli dwa
spsooby.
x2+y2=1
xy=24
3 cze 22:57
wredulus_pospolitus:
hęę
z drugiego wyznaczasz np. 'y' (założenie x≠0)
i to podstawiasz do pierwszego równania
pierwsze równanie przemnażasz obustronnie przez 'x
2'
robisz podstawienie t = x
2 ; t>0
rozwiązujesz to równianie kwadratowe (sprawdzasz z warunkiem t>0)
wracasz do podstawienia
wyznaczasz 'x'
wyznaczasz 'y'
3 cze 23:15
Eta:
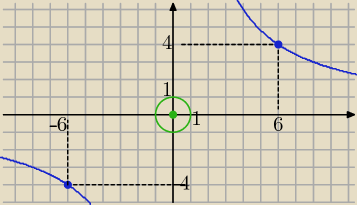
Ten układ nie ma rozwiązań !
3 cze 23:25
??: yle to też wiem. ale nie wychodzi mi to po prostu. bo wyjdzie x
2+y
2=1 pod spodem 2xy=48 potem
wtedy tylko wtedy x
2+2xy+y
2=1 pod spodem 2xy=48 wtedy tylko wtedy pote m x
2+2xy+
2=1+48 pod
sppde, x
2− 2xy+y
2=48−1 wtedy tylko wtedy uuu thdzue (x+y+ 7)(x+y−7)=0 pod spodem (x−y+peirw.
z 47 ) ( x−y−pierw. z 47.) róne zero aleee ma wyjść zbiór pusty w tmy i wtym wiec nie wiem
3 cze 23:26
ICSP: x2 + y2 = 1 ⇒ (x+y)2 − 2xy = 1 ⇒ (x+y)2 = 1 + 2xy ⇒ (x+y)2 = 49 ⇒ x+y = 7 v x+y = − 7
i mamy dwa układy równań :
x+y = 7
xy = 24
x+y = − 7
xy = 24
jak widać żaden z nich mie ma rozwiazania bo równanie kwadratowej z2 ± 7z + 24 nie ma
pierwiastków rzeczywistych.
3 cze 23:28
ICSP: równania kwadratowe*
3 cze 23:29
??: dzięki Eta. tylko ja to muszę zapisać a nie na rysować.
3 cze 23:29
??: dzięki Eta tylko ja to muszę zapisać a nie narysować.
3 cze 23:31
3 cze 23:36
ICSP: tobie wychodzi
x2 − 2xy + y2 = − 47
(x−y)2 = − 47
sprzeczność .
3 cze 23:36
wredulus_pospolitus:
.
to jak dojdziesz do wyznaczania pierwiastków 't'
to wyjdzie że oba pierwiastki będą <0 ... czyli brak rozwiązań
3 cze 23:38
wredulus_pospolitus:
albo wręcz ... nawet ten wielomian (od t) nie będzie miał rozwiązań
3 cze 23:39
??: noł. najpierw to dodajeee 1+48 iii x2+2xy+y2/ a potem to odejmuje.
3 cze 23:40
??: więc będzieeeeee dodatnia a nie ujemna
:(
3 cze 23:42
??: więc będzieeeeee dodatnia a nie ujemna
:(
3 cze 23:42
wredulus_pospolitus:
a po co dodajesz
myślimy trochę:
1)
x
2 + y
2 = 1
xy = 24
2)
x
2 + y
2 = 1
−2xy =
−2*24
3)
dodajesz równania
x
2 −2xy + y
2 = 1−48
(x−y)
2 = −47
3 cze 23:45
wredulus_pospolitus:
a jeżeli tego nie widzisz (nie wpadłbyś/−aś na to) to robisz 'standardowo' czyli tak jak
napisałem wcześniej i dojdziesz w końcu do sprzeczności
3 cze 23:46
pigor: ..., otóż np. tak :
x2+y2=1 i xy=24 ⇔ x
2+y
2=1 i 2xy=48 /+ stronami ⇔ (x+y)
2= 49 ⇔
⇔ |x+y|=7 ⇔ x+y=−7 lub x+y=7 ⇔ y=−x−7 lub y=−x+7 − dwie proste równoległe,
więc
(x,y) ∊ ∅ − szukana para nie istnieje; dany układ nie ma rozwiązania . ...
4 cze 08:49
pigor: ... , przepraszam powyżej pospieszyłem się , więc kończę np. tak :
x2+y2=1 i xy=24 ⇔ ... ⇔ (y=−x−7 lub y=−x+7) i xy=24 ⇔
⇔ x(−x−7)=24 lub x(−x+7)=24 ⇔ x
2+7x+24=0 lub x
2−7x+24=0 ale w obu równaniach
Δ= 49−4*24 < 0 , więc nie istnieją x, a tym samym y takie, że para (x,y) byłaby rozwiązaniem
danego układu równań okręgu i hiperboli ; po prostu układ jest sprzeczny . ...
4 cze 09:23
