Funkcja wymierna Kostek: Mam takie zadanko ze zbioru Norbert Dróbko, Karol Szymański i nie wiem jak rozwiązać Dla jakich wartości parametru k, w zbiorze rozwiązań danej nierówności jest zawarty przedział <−1,1>

x2+k2
	≥1
2k

PW: k≠0 (bo jest w mianowniku). W takim razie licznik jest dodatni (suma kwadratów). Zadana nierówność jest więc równoważna nierówności x²+k²≥2k, k>0 Nie ma sensu rozpatrywanie ujemnych k, gdyż dla takich k lewa strona nierówności jest ujemna (licznik dodatni, mianownik ujemny). Mamy zatem zwykłą nierówność kwadratową z dodatnim parametrem k: x²+(k²−2k)≥0, k>0. Trzeba tak dobrać k, żeby istniały dwa pierwiastki − jeden mniejszy lub równy −1, drugi większy lub równy 1.

PW: uu, to ostatnie zdanie to głupstwo. Narysuj parabolę i zobacz jakie mają być pierwiastki, żeby w rozwiązaniu był przedział <−1,1>. Może być też tak, że rozwiązaniem jest cały zbiór R (pierwiastków nie ma), a <−1,1>⊂R.

Mateusz: "Trzeba tak dobrać k, żeby istniały dwa pierwiastki − jeden mniejszy lub równy −1, drugi większy lub równy 1." To zdanie nie wydaje mi sie sensowne raczej trzeba tak dobrac miejsca zerowe aby rozwiązaniem był ow przedział

Mateusz: O widze ze poprawione wybacz nie widziałem kiedy pisałem

Kostek: OK dziękuje za odpowiedź

PW: To uroda rozwiązywania "on line". Trzymając w ręce pióro nie napisałbym wielu andronów, które już tutaj udało mi się popełnić. Dzięki, Mateuszu. Dobrze, że sprawdzamy się nawzajem.

pigor: ..., no to może tak : licznik zawsze ≥ 0 i całość ≥ 1 ⇒ (*) k>0 wtedy

x2+k2
	≥1 /* 2k ⇔ x2+k2 ≥ 2k ⇔ x2 ≥ 2k−k2 , ale −1 ≤ x ≤ 1 ⇔
2k

⇔ |x| ≤ 1 ⇔ x² ≤1 ⇒ 1 ≥ x² ≥ 2k−k² ⇒ 1 ≥ 2k−k² ⇔ k²−2k+1 ≥0 ⇔ ⇔ (k−1)² ≥ 0 ⇔ k∊R , to stąd i z (*) k∊R+ . ... −−−−−−−−−−−−−−−−−−− ciekawe jaką panowie D. i Sz. dali odpowiedź w zbiorze

Mateusz: Wiem PW kazdy moze sie pomylić

Kostek: pigor odpowiedź w zbiorze k≥2

Mila:

x2+k2
	≥1, k≠0
2k

x²+k²>0 dla każdego x i każdego k≠0⇒k>0

	x2+k2
		≥1 /*2k⇔
	2k

x²+k²≥2k⇔ x²+k²−2k≥0 i k>0 y=x²+k²−2k parabola symetryczna względem OY i skierowana do góry, aby <−1,1> zawierał się w zbiorze rozwiązań nierówności: x²+k²−2k≥0 to parabola musi leżeć nad osią OX.( brak pierwiastków) ⇔ k²−2k≥0⇔k(k−2)≥0⇔ k≤0 lub k≥2 i k>0⇔ k≥2

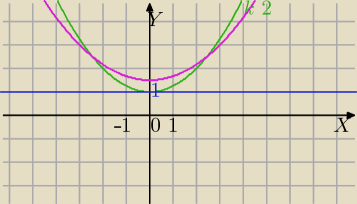
	x2+k2
ilustracja dla nierówności:		≥1
	2k

	x2+k2
y=		wykres dla k=2
	2k

	x2+k2
y=		wykres dla k=3
	2k

Kostek: Mila dziękuje bardzo

Mila: