
 łatwo , ale za to szybko
1) AB→= [3−1,5−1]= [2,4]= 2[1,2] i S= (12(1−1), 12(1+3))= (0,2) − środek AC,
więc 1(x−0)+2(y−2)=0 ⇔ x+2y−4=0 − szukane równanie prostej
−−−−−−−−−−−−−−−−−−−−−
2) h ⊥ AB i C∊h, więc h : 2(x+1)−1(y−3)=0 ⇔ 2x−y+5=0 − szukane równanie wysokości,
−−−−−−−−−−−−−−−−−−−−−−−−
3) S=(12(1+3), 12(1+5))= (2,3) − środek AB, więc s: 2(x−2)−1(y−3)=0 ⇔
⇔ 2x−4−y+3=0 ⇔ 2x−y−1=0 − szukane równanie symetralnej boku AB .. i to tyle ...
łatwo , ale za to szybko
1) AB→= [3−1,5−1]= [2,4]= 2[1,2] i S= (12(1−1), 12(1+3))= (0,2) − środek AC,
więc 1(x−0)+2(y−2)=0 ⇔ x+2y−4=0 − szukane równanie prostej
−−−−−−−−−−−−−−−−−−−−−
2) h ⊥ AB i C∊h, więc h : 2(x+1)−1(y−3)=0 ⇔ 2x−y+5=0 − szukane równanie wysokości,
−−−−−−−−−−−−−−−−−−−−−−−−
3) S=(12(1+3), 12(1+5))= (2,3) − środek AB, więc s: 2(x−2)−1(y−3)=0 ⇔
⇔ 2x−4−y+3=0 ⇔ 2x−y−1=0 − szukane równanie symetralnej boku AB .. i to tyle ... 
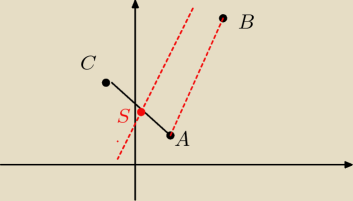 1) środek boku AC⇒S
2) współczynnik kierunkowy AB
3) równanie równoległej do AB przechodzącej przez S
1) środek boku AC⇒S
2) współczynnik kierunkowy AB
3) równanie równoległej do AB przechodzącej przez S
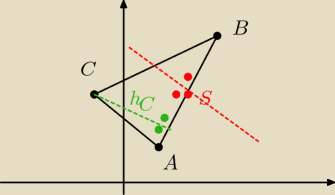 2) zielony
3) czerwony kolor
2) zielony
3) czerwony kolor