


 proszę o pomoc
proszę o pomoc

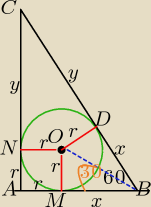 ∡ABC=600
∡BAC=900
r− promień okręgu wpisanego w ΔABC
T:
AC*AB=2*CD*BD
D − punkt styczności okręgu z przeciwprostokątną
Punkty styczności M i D są jednakowo odległe od wierzchołka B
Punkty styczności M i A są jednakowo odległe od wierzchołka A
Punkty styczności N i D są jednakowo odległe od wierzchołka C
W ΔOMB:
∡ABC=600
∡BAC=900
r− promień okręgu wpisanego w ΔABC
T:
AC*AB=2*CD*BD
D − punkt styczności okręgu z przeciwprostokątną
Punkty styczności M i D są jednakowo odległe od wierzchołka B
Punkty styczności M i A są jednakowo odległe od wierzchołka A
Punkty styczności N i D są jednakowo odległe od wierzchołka C
W ΔOMB:
| r | ||
tg300= | ||
| x |
| √3 | r | ||
= | |||
| 3 | x |
| AC | ||
tg600= | ||
| AB |
| AC | |
=√3⇔AC=r(√3+3) | |
| r(1+√3) |
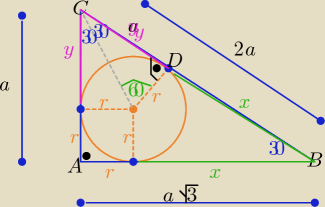 y=|DC|= r√3 , a= |AC|= y+r= r(√3+1)
|BC|=x+y= 2a ⇒ x=|BD|= 2r(√3+1) −r√3= r(√3+2)
|AB|= r+x = r(√3+3)
sprawdzamy równość : |AB|*|AC|= 2|BD|*|DC|
L= |AB|*|AC| = r(√3+3)*r(√3+1) = ....=2r2(2√3+3)
P= 2*|BD|*|DC|= 2*r(√3+2)*r√3= 2r2(2√3+3)
L=P taka równość zachodzi
Pewnie jest prostszy dowód ( póki co ....... myślę)
P.S taka równość zachodzi, bez względu na miary kątów ostrych!
Jutro podam dowód
y=|DC|= r√3 , a= |AC|= y+r= r(√3+1)
|BC|=x+y= 2a ⇒ x=|BD|= 2r(√3+1) −r√3= r(√3+2)
|AB|= r+x = r(√3+3)
sprawdzamy równość : |AB|*|AC|= 2|BD|*|DC|
L= |AB|*|AC| = r(√3+3)*r(√3+1) = ....=2r2(2√3+3)
P= 2*|BD|*|DC|= 2*r(√3+2)*r√3= 2r2(2√3+3)
L=P taka równość zachodzi
Pewnie jest prostszy dowód ( póki co ....... myślę)
P.S taka równość zachodzi, bez względu na miary kątów ostrych!
Jutro podam dowód 
 Witaj Mila
Witaj Mila 

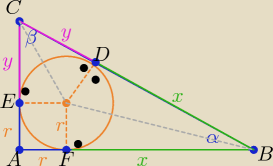 |AC|= y+r , |AB|= x+r , |BC|=x+y
z tw. Pitagorasa (x+r)2+(y+r)2=(x+y)2
2xr+r2+2yr+r2= 2xy :2
xr+yr+r2= xy= |BD|*|DC|
|AC|= y+r , |AB|= x+r , |BC|=x+y
z tw. Pitagorasa (x+r)2+(y+r)2=(x+y)2
2xr+r2+2yr+r2= 2xy :2
xr+yr+r2= xy= |BD|*|DC|
| |AC|*|AB| | ||
P(ABC)= | ||
| 2 |
| (y+r)(x+r) | xy | xr+yr+r2 | xy | xy | ||||||
P= | = | + | = | + | = xy | |||||
| 2 | 2 | 2 | 2 | 2 |
| |AC|*|AB| | ||
to | = xy ⇒ |AC|*|AB|= 2xy = 2*|BD|*|DC| | |
| 2 |