Przekroje ostroslupow Przemek.G: Przez krawędź podstawy ostroslupa prawidłowego czworokatnego poprowadzono płaszczyznę prostopadłą do przeciwległej ściany bocznej. Oblicz pole otrzymanego przekroju, jeśli długości krawędzi podstawy wynosi 10, a krawędzi bocznej ostroslupa 13

Mila: Masz odpowiedź?

Przemek.G: 2975 √7/432

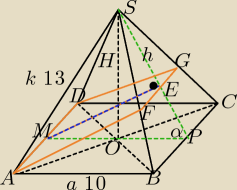
Mila: Przekrój jest trapezem równoramiennym

	|AD|+|FG|
P=		*|ME|
	2

h− wysokość ściany bocznej h²+|PC|²=|SC|² h²=13²−5²=169−25=144⇔h=12 H− wysokość ostrosłupa H²+5²=h² H²=144−25=119⇔ H=√119 W ΔSOP:

	H		5
Sinα=		; cosα=
	h		12

	√119
sinα=
	12

W ΔMEP:

	ME		ME		ME		√119		5√119
sinα=		=		⇔		=		⇔|ME|=
	MP		10		10		12		6

	EP		EP		EP		5		25
cosα=		=		⇔		=		⇔|EP|=
	MP		10		10		12		6

	25		1		5		47
SE=12−		=12−4		=7		=
	6		6		6		6

	SE		SP		SE		12
ΔSEF∼ΔSPB⇒		=		⇔		=		⇔
	FE		BP		FE		5

12|FE|=5*|SE|

	47
12|FE|=5*
	6

	235
|FE|=
	72

	235
|FG|=
	36

	235   10+   36		5√119
P=		*
	2		6

	19		5√119		595		5√119
P=16		*		=		*
	36		6		36		12

	2975√119
P=
	432