
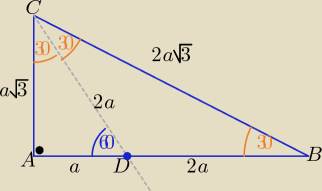
 Można tak: ze związków miarowych w trójkącie o kątach : 30o, 60o, 90o
|AC|= a√3 , |AD|= a , |DC|= 2a
ponieważ trójkąt BDC jest równoramienny to: |DB|=|DC|= 2a
zatem: |CB|= 2a√3
sprawdzamy daną równość:
L= |CB|2−2|DB|2= (2a√3)2−2(2a)2= 4a2*3−2*4a2= 4a2
P= |AD|2+|AC|2= a2+(a√3)2= a2+3a2= 4a2
L=P , zatem taka równość jest spełniona
c.n.u
Można tak: ze związków miarowych w trójkącie o kątach : 30o, 60o, 90o
|AC|= a√3 , |AD|= a , |DC|= 2a
ponieważ trójkąt BDC jest równoramienny to: |DB|=|DC|= 2a
zatem: |CB|= 2a√3
sprawdzamy daną równość:
L= |CB|2−2|DB|2= (2a√3)2−2(2a)2= 4a2*3−2*4a2= 4a2
P= |AD|2+|AC|2= a2+(a√3)2= a2+3a2= 4a2
L=P , zatem taka równość jest spełniona
c.n.u
 a dałoby się to zrobić z zależności pomiędzy funkcjami trygonometrycznymi
a dałoby się to zrobić z zależności pomiędzy funkcjami trygonometrycznymi 

 P.S.
Co znaczy skrót c.n.u ?
P.S.
Co znaczy skrót c.n.u ?
 for YOU
for YOU
| |AD| | a | 1 | ||||
sin30o= | ⇒ | = | ⇒ |DC|= 2a | |||
| |DC| | ||DC| | 2 |
| |AC| | |AC| | √3 | ||||
sin60o= | ⇒ | = | ⇒ |AC|= a√3 | |||
| |DC| | 2a | 2 |
| |AC| | a√3 | 1 | ||||
sin30o= | ⇒ | = | ⇒ |BC|= 2a√3 | |||
| |BC| | |BC| | 2 |



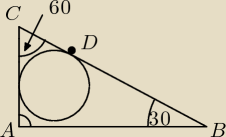 Mam jeszcze coś takiego:
W trójkąt prostokątny ABC o kącie ostrym 60 stopni wpisano okrąg. Punkt styczności D tego
okręgu z przeciwprostokątną CB dzieli ją na dwa odcinki CD i DB. Wykaż, że
|AC| * |AB| = 2 * |CD| * |DB|
Mam jeszcze coś takiego:
W trójkąt prostokątny ABC o kącie ostrym 60 stopni wpisano okrąg. Punkt styczności D tego
okręgu z przeciwprostokątną CB dzieli ją na dwa odcinki CD i DB. Wykaż, że
|AC| * |AB| = 2 * |CD| * |DB|




