Przekształcenia wektorów. Wiola: 1. Wierzchołki trójkąta ABC mają współrzędne: A(1,1), B(−2,7), C(−3,−1). Oblicz pole koła opisanego na trójkącie ABC. 2.Wyznacz wartość parametrów m i n, wiedząc, że wektory a i b są równe: a)wektor a=[2m+n,m−3n], wektor b=[m−1,5−n] 3.Wyznacz wartość parametrów m i n, wiedząc, że wektory a i b są przeciwne: a)wektor a=[3m−4,m−8], wektor b=[m+2n,m−2n]

bezendu: Rozwiązuje 1

Janek191: Rozwiązuję 2.

Eta: To ja 3/

Eta: → → 3/ a= − b ⇔ 3m−4= −m−2n i m−8= −m+2n teraz tylko rozwiąż ten układ równań ........

Janek191: Jeżeli te wektory są równe, to mają takie same współrzędne, czyli 2 m + n = m − 1 ⇒ n = − m −1 m − 3 n = 5 − n ⇒ 2n = m − 5 −−−−−−−−−−−−−−−−−−−− n = − m − 1 2*( − m − 1) = m − 5 −−−−−−−−−−− − 2 m − 2 − m = − 5 −3 m = − 3 m = 1 −−−− n = − 1 − 1 = − 2 −−−−−−−−−−−− Odp. m = 1, n = − 2 ===================

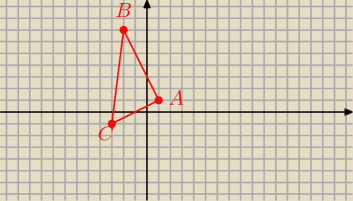
bezendu: Promień okręgu opisanego na tym trójkącie

	|AC|*|BC|*|AC|
R=
	PABC

|AC|=√−3−1)²+(−1−1)²=2√5 |AB|=√(−2−1)²+(7−1)²=3√5 |BC|=√(−3+2)²+(−1−7)²=√65 prosta przechodząca przez bok AB a+b=1 /(−1) −2a+b=7 −a−b=−1 −2a+b=7 −3a=6 a=−2 −2+b=1 b=3 y=−2x+3 zaraz reszta rozwiązania

Janek191: To jest trójkąt prostokątny, więc P = 0,5 * 2√5*3 √5 = 15

Janek191:

	1
R =		I BC I = 0,5 √65
	2

=======================

Janek191: Pole koła opisanego P = π R² = π * [ 0,5 √65)² = 0,25*65*π = 16,25 π j² =============================================

bezendu: teraz prosta CD która jest prostopadła do prostej AB i przechodzi przez punkt C

	1
y=		+b
	2

1
	*(−3)+b=−1
2

	3
−		+b=−1
	2

	1
b=
	2

	1		1
y=−		x+
	2		2

Punkt D

	1		1
−2x+3=		x+
	2		2

−2,5x=−2,5 x=1 y=1 więc punkt D=(1,1) długość odcinka |CD|=√(1+3)²+(1+1)²=2√5

	1
pole trójkąta PABC=		*|AB|*|CD|=15
	2

	3√5*√65*2√5
promień =		=2√65
	15

Pole koła P=π*R² P=(2√65)²*π=260π

Janek191: @bezendu Podany wzór na R jest błędny

Wiola: R = 1/2 I BC I = 0,5 √65 Skąd wziął się √65 ?

Janek191: bezendu wyliczył I BC I