Funkcja wymierna z parametrem Puzon: Wyznacz wartości parametru m, dla których równanie |x+3|=^m_m−4 ma dwa pierwiastki różnych znaków

Puzon: Czy wystarczy zauważyć, że w w module liczba musi być większa od 3, więc x>0 ?

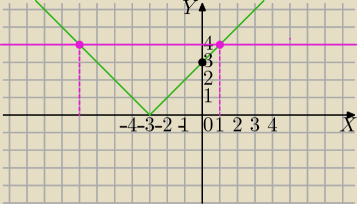
Mila: f(x)=|x+3|

	m
g(m)=
	m−4

m−4≠0⇔m≠4 1) Rysuję wykres funkcji f(x) 2)y= g(m) Dla g(m)>3 równanie

	m
|x+3|=		ma dwa rozwiązania o różnych znakach
	m−4

	m
g(m)>3 i m≠4⇔		>3
	m−4

Potrafisz rozwiązać tę nierówność? Odp. m∊(4,6)

ZKS: Pierwszy sposób.

	m
Zakładamy że		≥ 0 ⇒ m ∊ ...
	m − 4

Rysujemy wykres funkcji f(x) = |x + 3| zauważamy że wykres ten przecina oś OY w punkcie A = (0 ; 3) tak więc jeżeli y > 3 to argumenty będą różnych znaków. Czyli

	m
należy zapisać warunek w formie nierówności		> 3 pamiętając że
	m − 4

m
	≥ 0.
m − 4

Drugi sposób

	m
Robimy te samo założenie		≥ 0 i podnosimy obustronnie do kwadratu.
	m − 4

	m
|x + 3| =		/ 2
	m − 4

	m2
(x + 3)2 =		/ * (m − 4)2
	(m − 4)2

teraz wykonujemy przekształcenia równoważne (m − 4)²x² + 6(m − 4)²x + 3(m − 4)² = m² (m − 4)²x² + 6(m − 4)²x + 3(m − 4)² − m² = 0 Jak widzimy otrzymaliśmy funkcję kwadratową teraz aby otrzymać pierwiastki różnych znaków musimy dać założenia Δ > 0 ∧ x₁x₂ > 0. Rozwiązując te założenia powinniśmy otrzymać rozwiązanie pamiętając o założeniu początkowym. Trzeci sposób. Zakładamy jak w dwóch pierwszych przypadkach. Teraz rozpisujemy wartość bezwzględną.

	m		m
x + 3 =		∨ x + 3 = −
	m − 4		m − 4

	m		m
x =		− 3 ∨ x = −		− 3
	m − 4		m − 4

Zauważamy że pierwsze wyrażenie musi mięć większy pierwiastek i dodatni

	m
(ponieważ		≥ 0 i warunki o dwóch pierwiastkach różnych znaków).
	m − 4

Zapisujemy ten warunek w formie nierówności

m
	− 3 > 0.
m − 4

Teraz skoro zapisaliśmy że wyrażenie pierwsze ma dodatni pierwiastek to musimy to samo zrobić z drugim wyrażeniem aby miał ujemny pierwiastek czyli

	m
−		− 3 < 0.
	m − 4

Biorąc iloczyn (część wspólną) tych zbiorów nierówności otrzymujemy rozwiązanie.

ZKS: Oczywiście warunek w drugim sposobie o pierwiastkach różnych znaków to x₁x₂ < 0.