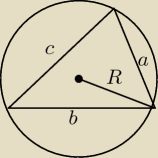
Twierdzenie sinusów malgoosiak: Uzasadnij, korzystając z twierdzenia sinusów, że pole dowolnego trójkąta o bokach: a, b, c wyraża się za pomocą wzoru

	abc
P=
	4R

gdzie R jest promieniem okręgu opisanego na tym trójkącie.

Eta:

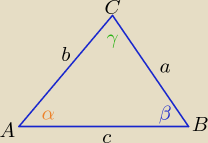
a		a		b		c
	=2R ⇒ sinα=		i sinβ=		i sinγ=
sinα		2R		2R		2R

	1		1		a		abc
P(ABC)=		bc*sinα=		bc*		=
	2		2		2R		4R

podobnie

	1		abc		1		abc
P(ABC)=		ac*sinβ=		i P(ABC)=		ab*sinγ=
	2		4R		2		4R

	abc
zatem P(ABC)=
	4R

R −− długość promienia okręgu opisanego na trójkącie ABC o bokach długości a,b,c

Mila: Z tw. sinusów :

a		a
	=2R⇔a=2R *sinα⇔sinα=
sinα		2R

	1		1		a
PΔ=		b*c*sinα=		b*c*		⇔
	2		2		2R

	abc
PΔ=
	4R