Trójkąty przystające xantor: Na jednej z dwóch prostych przecinających się w punkcie O odkładamy dwa odcinki OA i OB, gdzie IOAI = IOBI. Na drugiej prostej odkładamy dwa inne odcinki OC i OD takie, że IOCI = IODI. Wykaż, że pr. AC II pr. BD.

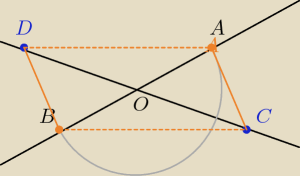
Mila: W czworokącie ACBD przekątne dzielą się na połowy, zatem czworokąt ACBD jest równoległobokiem AC||BD jako przeciwległe boki równoległoboku ACBD.

xantor: dzięki ale ja chciałbym te zadanie z cechy trójkątów przystających

Mila: Możesz uzasadnić, że w czworokącie ACBD, boki przeciwległe są rowne, zatem jest to rownoległobok. ΔAOC=ΔBOD cecha bkb⇔AC=DB ΔAOD=ΔCOB cecha bkb⇔BC=AD⇔czworokąt ACBD jest równoległobokiem, zatem boki przeciwległe są rownoległe⇔ AC||BD

Mila: ?

xantor: to dobry pomysł dziękować