pole prostokąta
zdesperowana:
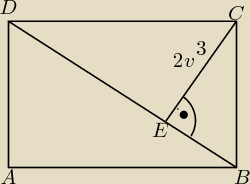
W prostokącie ABCD poprowadzono przekątną BD i obrano na niej taki punkt E, że odcinek CE jest
prostopadły do tej przekątnej i dzieli ją w skali 2:1 . Oblicz pole prostokąta ABCD wiedząc,
że długość odcinka CE jest równa 2√3.
Bardzo proszę o pomoc.
1 cze 19:10
Eta:
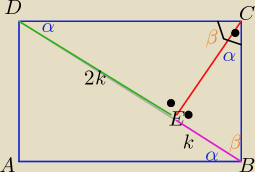
z podobieństwa trójkątów BEC i DEC z cechy (kkk)
|CE|
2= 2k*k , k>0
(2
√3)
2= 2k
2 ⇒ k
2= 6 ⇒ k=
√6
|BD|= 3k = 3
√6
P(ABCD)= |BD|*|CE|=..................
1 cze 19:26
agulka:
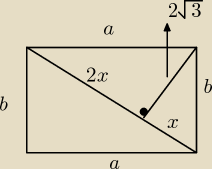
P=a*b
a
2+b
2=(3x)
2
1
0 a
2+b
2=9x
2
2
0 a
2=(2x)
2+(2
√3)
2⇒a
2=4x
2+12
3
0 b
2=x
2+(2
√3)
2⇒b
2=x
2+12
Równania 2
0 i 3
0 wstawiam do równania 1
0:
4x
2+12+x
2+12=9x
2
x
2=6⇒x=
√6
a
2=4*6+12=36⇒a=6
b
2=6+12=18⇒b=3
√2
P=6*3
√2=18
√2
1 cze 20:01
Eta:
@
agulka
A co ja innego podałam ?

1 cze 20:06
agulka: A kto tu mówi, że ty coś innego podałas? Ja podałam po prostu inny sposób bez uwzględniania
podobieństwa trójkątów
1 cze 20:10
Eta:
Jeżeli już to "Ty" a nie "ty"

1 cze 20:12
agulka: Trochę kultury i pokory. Nie jesteś tu sama na tym forum. Niektórzy też mają inne pomysły na
rozwiązywanie zadań i wcale nie oznacza to,że gorsze
1 cze 20:22
zdesperowana: po co te kłótnie

dziękuję bardzo Wam obydwóm!
1 cze 22:20
asia: 1.Zapisz wyrażenia w jak najprostszej postaci.
a) (1−cos α)(1+cos α)
1
b) −−−−−−− − sin α * tg α
cos α
23 paź 17:48
Beata: a)(1−cosα)(1+cosα) = 1−cos2α=sin2α
b) założenie: cosα≠0;
1/cosα − sinα* tgα = 1/cosα − sinα* (sinα/cosα) = 1/cosα − sin2α/cosα=(1−sin2α)/cosα=
cos2α/cosα= cosα
23 paź 18:27
 W prostokącie ABCD poprowadzono przekątną BD i obrano na niej taki punkt E, że odcinek CE jest
prostopadły do tej przekątnej i dzieli ją w skali 2:1 . Oblicz pole prostokąta ABCD wiedząc,
że długość odcinka CE jest równa 2√3.
Bardzo proszę o pomoc.
W prostokącie ABCD poprowadzono przekątną BD i obrano na niej taki punkt E, że odcinek CE jest
prostopadły do tej przekątnej i dzieli ją w skali 2:1 . Oblicz pole prostokąta ABCD wiedząc,
że długość odcinka CE jest równa 2√3.
Bardzo proszę o pomoc.
 z podobieństwa trójkątów BEC i DEC z cechy (kkk)
|CE|2= 2k*k , k>0
(2√3)2= 2k2 ⇒ k2= 6 ⇒ k= √6
|BD|= 3k = 3√6
P(ABCD)= |BD|*|CE|=..................
z podobieństwa trójkątów BEC i DEC z cechy (kkk)
|CE|2= 2k*k , k>0
(2√3)2= 2k2 ⇒ k2= 6 ⇒ k= √6
|BD|= 3k = 3√6
P(ABCD)= |BD|*|CE|=..................
 P=a*b
a2+b2=(3x)2
10 a2+b2=9x2
20 a2=(2x)2+(2√3)2⇒a2=4x2+12
30 b2=x2+(2√3)2⇒b2=x2+12
Równania 20 i 30 wstawiam do równania 10:
4x2+12+x2+12=9x2
x2=6⇒x=√6
a2=4*6+12=36⇒a=6
b2=6+12=18⇒b=3√2
P=6*3√2=18√2
P=a*b
a2+b2=(3x)2
10 a2+b2=9x2
20 a2=(2x)2+(2√3)2⇒a2=4x2+12
30 b2=x2+(2√3)2⇒b2=x2+12
Równania 20 i 30 wstawiam do równania 10:
4x2+12+x2+12=9x2
x2=6⇒x=√6
a2=4*6+12=36⇒a=6
b2=6+12=18⇒b=3√2
P=6*3√2=18√2


 dziękuję bardzo Wam obydwóm!
dziękuję bardzo Wam obydwóm!